
【题目】如图P为等边△ABC外一点,AH垂直平分PC于点H,∠BAP的平分线交PC于点D
(1) 求证:DP=DB
(2) 求证:DA+DB=DC
(3) 若等边△ABC边长为![]() ,连接BH,当△BDH为等边三角形时,请直接写出CP的长度为_________
,连接BH,当△BDH为等边三角形时,请直接写出CP的长度为_________

【答案】(1)证明见解析(2)证明见解析 (3) ![]()
【解析】试题分析:(1)首先由等边三角形的性质易得AB=AC=BC,由垂直平分线的性质易得AP=AC,即AP=AB,由SAS可证得△PAD≌△BAD,利用全等三角形的性质可得结论;
(2)在CP上截取CQ=PD,证明△ACQ≌△APD,利用全等三角形的性质可得△ADQ是等边三角形,得出结论;
(3)连接BH,延长AD交PB于点E,根据PA=PB,AD是角平分线得出AE⊥PB,且平分PB,由△BDH是等边三角形,知PD=BD,易得BD=DH=BH,∠BPH=30°,然后根据30°角的直角三角形的三角函数和勾股定理可求解.
试题解析:(1) ∵AH是PC的垂直平分线
∴PA=PC=AB
∵AD平分∠PAB
∴∠PAD=∠BAD
在△PAD和△BAD中, 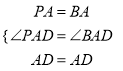
∴△PAD≌△BAD(SAS)
∴DP=DB
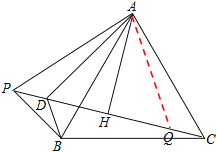
(2) 在CP上截取CQ=PD,连接AQ
∵AP=AC
∴∠APD=∠ACQ
在△APD和△ACQ中, 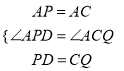
∴△APD≌△ACQ(SAS)
∴AD=AQ,∠CAQ=∠PAD
∴∠BAC=∠CAQ+∠BAQ=∠PAD+∠BAQ=∠BAD+∠BAQ=∠DAQ=60°
∴△ADQ为等边三角形
∴AD=DQ
∴CD=DQ+CQ=AD+DB
(3) ![]() (提示:设DP=DB=DH=x,则CH=2x,CD=3x,AD=CD-DB=2x)
(提示:设DP=DB=DH=x,则CH=2x,CD=3x,AD=CD-DB=2x)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】中新社北京1月13日电,北京市气象台发布北京气象史上首个雾霾橙色预警,北京已连续3天空气质量达严重污染中的“最高级”——六级污染.雾霾(PM2.5)含有大量的有毒有害物质,对人体健康有很大的危害,被称为大气元凶.雾霾的直径大约是0.000 002 5m ,把数据0.000 002 5用科学记数法表示为_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,∠C=90°,∠A=30°.
中,∠C=90°,∠A=30°.
(1)尺规作图:作线段AB的垂直平分线l(保留作图痕迹,不写作法);
(2)在已作的图形中,若l分别交AB、AC及BC的延长线于点D、E、F,连接BE,求证:EF=2DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公园内两条小河MO,NO在O处汇合,两河形成的半岛上有一处景点P(如图所示).现计划在两条小河上各建一座小桥Q和R,并在半岛上修三段小路,连通两座小桥与景点,这两座小桥应建在何处才能使修路费用最少?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线y=-x2+bx+c经过A(0,-2),B(-1,1)两点,那么此抛物线经过
A. 第一、二、三、四象限 B. 第一、二、三象限
C. 第一、二、四象限 D. 第二、三、四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:我们知道一元二次方程是转化为一元一次方程来解的,例如:解方程![]() ,通过因式分解将方程化为
,通过因式分解将方程化为![]() ,从而得到
,从而得到![]() =0或
=0或![]() 两个一元一次方程,通过解这两个一元一次方程,求得原方程的解.
两个一元一次方程,通过解这两个一元一次方程,求得原方程的解.
(1)利用上述方法解一元二次不等式: ![]() ;
;
(2)利用函数的观点解一元二次不等式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com