

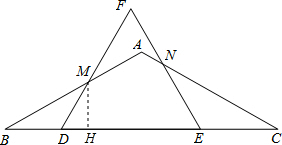
 (2)解:过点M作MH⊥BC,
(2)解:过点M作MH⊥BC,| MH |
| MD |
| 4-x |
| x |
| ||
| 2 |
| 3 |
| 3 |
 (3)解:过点M作MH⊥BC于H,过点A作AK⊥BC于K,
(3)解:过点M作MH⊥BC于H,过点A作AK⊥BC于K,| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
4
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| 3 |
16
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| BD |
| CE |
| x2 |
| (4-x)2 |
| ||
| 4 |
16
| ||
| 3 |
| ||
| 4 |
| ||
| 4 |
| ||
| 2 |
| 3 |
4
| ||
| 3 |
| ||
| 2 |
10
| ||
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
10
| ||
| 3 |


科目:初中数学 来源: 题型:
 (2012•娄底)如图,在一场羽毛球比赛中,站在场内M处的运动员林丹把球从N点击到了对方内的B点,已知网高OA=1.52米,OB=4米,OM=5米,则林丹起跳后击球点N离地面的距离NM=
(2012•娄底)如图,在一场羽毛球比赛中,站在场内M处的运动员林丹把球从N点击到了对方内的B点,已知网高OA=1.52米,OB=4米,OM=5米,则林丹起跳后击球点N离地面的距离NM=查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•娄底)如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.5米,求这棵树AB的高度(结果保留两位有效数字,
(2012•娄底)如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.5米,求这棵树AB的高度(结果保留两位有效数字,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•娄底)如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(2012•娄底)如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•娄底)如图,A、B的坐标分别为(1,0)、(0,2),若将线段AB平移到至A1B1,A1、B1的坐标分别为(2,a)、(b,3),则a+b=
(2012•娄底)如图,A、B的坐标分别为(1,0)、(0,2),若将线段AB平移到至A1B1,A1、B1的坐标分别为(2,a)、(b,3),则a+b=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com