
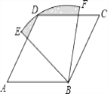
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是______
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形网格中每个小正方形边长都是1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形:
![]() 在网格中画出长为
在网格中画出长为![]() 的线段AB.
的线段AB.
![]() 在网格中画出一个腰长为
在网格中画出一个腰长为![]() 、面积为3的等腰
、面积为3的等腰![]() DEF.
DEF.
(3)利用网格,可求出三边长分别为![]() ,
,![]() ,
,![]() 的三角形面积为__________
的三角形面积为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
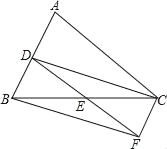
【题目】已知:如图,在△ABC中,D、E分别是AB、BC边上的中点,过点C作CF∥AB,交DE的延长线于F点,连接CD、BF.
(1)求证:△BDE≌△CFE;
(2)△ABC满足什么条件时,四边形BDCF是矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆最大载重48吨的大型货车,货车的货箱是长14m,宽2.5m,高3m的长方体,现有甲种货物18吨,乙种货物70m3,而甲种货物每吨的体积为2.5m3,乙种货物每立方米0.5吨.问:
(1)甲、乙两种货物是否都能装上车?请说明理由.
(2)为了最大地利用车的载重量和货箱的容积,两种货物应各装多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有数字1、2、3的蓝色卡片,卡片除颜色和数字外其它完全相同。
(1)从中任意抽取一张卡片,则该卡片上写有数字1的概率是;
(2)将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于22的概率。(请利用树状图或列表法说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
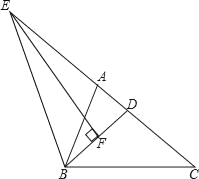
【题目】在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于点E.
(1)求证:ED2=EAEC;
(2)若ED=6,BD=CD=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a,b分别是数轴上两个不同点A,B所表示的有理数,且|a|=5,|b|=2,A,B两点在数轴上的位置如图所示:
![]()
(1)试确定数a,b;
(2)A,B两点相距多少个单位长度?
(3)若C点在数轴上,C点到B点的距离是C点到A点距离的![]() ,求C点表示的数;
,求C点表示的数;
(4)点P从A点出发,先向左移动1个单位长度,再向右移动2个单位长度,再向左移动3个单位长度,再向右移动4个单位长度,依次操作2 019次后,求P点表示的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com