
【题目】如图所示,在Rt△ABC中,∠BAC=90°,∠B=45°,O为BC中点,如果点M、N分别在线段AB、AC上移动,设AM长为x,CN的长为y,且x、y满足等式![]() =0(a>0).
=0(a>0).
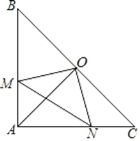
(1)求证:BM=AN;
(2)请你证明△OMN为等腰直角三角形.
【答案】(1)见解析;(2)见解析
【解析】
(1)由等式可得出x=y=a,结合等腰直角三角形的性质,即可证得;
(2)作OE⊥AC,OF⊥AB,通过证明△OFM≌△OEN,可得OM=ON,根据全等三角形的性质,只要证得∠MON=90°,即可证得.
证明:(1)∵x、y满足等式![]() =0(a>0),
=0(a>0),
∴x=y=a,即AM=CN=a,
∵Rt△ABC中,∠BAC=90°,∠B=45°,
∴AB=AC,
∴BM=AN;
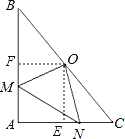
(2)作OE⊥AC,OF⊥AB,
∴∠OFM=∠ONE=∠FOE=90°,
∵点O是BC的中点,
∴OE=OF=![]() AB=
AB=![]() AC,AF=BF,AE=CE,
AC,AF=BF,AE=CE,
∴OF=OE,AF=CE,
∴AF﹣AM=CE﹣CN,
∴MF=NE,
∴在△OFM和△OEN中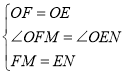 ,
,
∴△OFM≌△OEN(SAS),
∴OM=ON,∠MOF=∠NOE,
∵∠FOM+∠MOE=90°,
∴∠MOE+∠NOE=∠MON=90°,
∴△OMN是等腰直角三角形.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
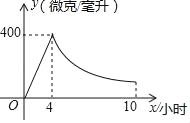
【题目】驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾,某研究所经实验测得:成人饮用某品牌38度白酒后血液中酒精浓度y(微克/毫升)与饮酒时间x(小时)之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中酒精浓度上升和下降阶段y与x之间的函数表达式.
(2)问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,8),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )
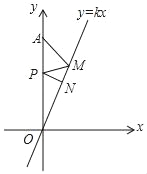
A. 4 B. 4![]() C. 8sin40° D. 8sin20°(1+cos20°+sin20°cos20°)
C. 8sin40° D. 8sin20°(1+cos20°+sin20°cos20°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=![]() ,AD=1.
,AD=1.
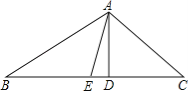
(1)求BC的长;
(2)求tan∠DAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
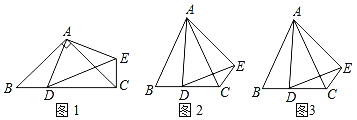
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=_____度;如图2,当点D在线段BC上,如果∠BAC=60°,则∠BCE=______度.
(2)设∠BAC=α,∠BCE=β,如图3,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2-2ax+c与x轴交于A,B两点,与y轴正半轴交于点C,且A(-1,0).
(1)一元二次方程ax2-2ax+c=0的解是 ;
(2)一元二次不等式ax2-2ax+c>0的解集是 ;
(3)若抛物线的顶点在直线y=2x上,求此抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州市处于东南沿海,夏季经常遭受台风袭击,一次,温州气象局测得台风中心在温州市![]() 的正西方向300千米的
的正西方向300千米的![]() 处,以每小时
处,以每小时![]() 千米的速度向东偏南
千米的速度向东偏南![]() 的
的![]() 方向移动,距台风中心200千米的范围是受台风严重影响的区域,试问:
方向移动,距台风中心200千米的范围是受台风严重影响的区域,试问:
(1)台风中心在移动过程中离温州市最近距离是多少千米?
(2)温州市![]() 是否受台风影响?若不会受到,请说明理由;若会受到,求出温州市受台风严重影响的时间.
是否受台风影响?若不会受到,请说明理由;若会受到,求出温州市受台风严重影响的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com