
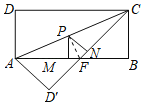
【题目】如图,长方形ABCD中,AB=6,AC=3![]() ,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.点P为线段AC(不含点A、C)上任意一点,PM⊥AB于点M,PN⊥CD′于点N,PM+PN=_____.
,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.点P为线段AC(不含点A、C)上任意一点,PM⊥AB于点M,PN⊥CD′于点N,PM+PN=_____.

【答案】3
【解析】
根据矩形的性质和翻折变换的性质得到AF=CF,设AF=x,根据勾股定理列出方程,解方程即可求出AF,再根据三角形的面积公式解答即可.
解:连接PF,如图所示:
∵四边形ABCD是矩形
∴∠B=90°,AB∥CD,
∴BC=![]() =
=![]() =3,∠DCA=∠BAC,
=3,∠DCA=∠BAC,
∵矩形沿AC折叠,点D落在点E处,
∴△ACD≌△ACE,
∴∠DCA=∠ECA,
∴∠BAC=∠ECA,
∴AF=CF,
设AF=CF=x,则BF=6﹣x,
在Rt△BCF中,根据勾股定理得:BC2+BF2=CF2,
即32+(6﹣x)2=x2,
解得:x=![]() ,
,
∴AF=![]()
∴S△ACF=![]() AFBC=
AFBC=![]() ×
×![]() ×3=
×3=![]() ,
,
∵![]() ×AF×PM+
×AF×PM+![]() ×CF×PN=S△ACF=
×CF×PN=S△ACF=![]() ,
,
∴![]() ×
×![]() ×(PM+PN)=
×(PM+PN)=![]() ,
,
∴PM+PN=3;
故答案为:3.


科目:初中数学 来源: 题型:
【题目】已知:在矩形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() 分别在矩形
分别在矩形![]() 边
边![]() 、
、![]() 、
、![]() 上,
上,![]() .
.
![]() 如图
如图![]() ,当四边形
,当四边形![]() 为正方形时,求
为正方形时,求![]() 的面积;
的面积;
![]() 如图
如图![]() ,当四边形
,当四边形![]() 为菱形时,设
为菱形时,设![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域.
的函数关系式,并写出函数的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,将两边AD与BC平行的纸条ABCD沿BD折叠,使点C落在C′处,AD与BC′相交于点E.

(1)求证:BE=DE;
(2)如图②,分别过点B,D作BM⊥AD,DN⊥BC′,垂足分别为M,N.求证:△BMD≌△DNB;
(3)若BM=4cm,DM=8cm,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )

A. 4 B. 8 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com