
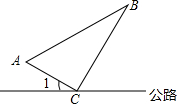
 如图,在公路的同侧有A、B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5km/h,问多长时间后这人距离B送奶站最近?
如图,在公路的同侧有A、B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5km/h,问多长时间后这人距离B送奶站最近? 分析 首先根据勾股定理逆定可证明△ABC是直角三角形,然后计算出∠BCD的度数,再根据直角三角形的性质算出DC的长,然后根据速度和路程可计算出多长时间后这人距离B送奶站最近.
解答 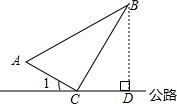 解:∵82+152=172,
解:∵82+152=172,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°,
∵∠1=30°,
∴∠BCD=180°-90°-30°=60°,
在Rt△BCD中,∵∠BCD=60°,
∴∠CBD=30°,
∴CD=$\frac{1}{2}$BC=$\frac{1}{2}×15$=7.5(km),
∵7.5÷2.5=3(h),
∴3小时后这人距离B送奶站最近.
点评 此题主要考查了勾股定理逆定理以及直角三角形的性质,关键是掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
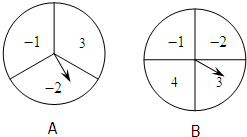 如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.同时转动两个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作m,将B转盘指针指向的数字记作n.
如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.同时转动两个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作m,将B转盘指针指向的数字记作n.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y3<y2<y1 | B. | y2<y1<y3 | C. | y1<y2<y3 | D. | y2<y3<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com