练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】三江夜游项目是宁波市月光经济和“三江六岸”景观提升的重要工程，一艘游轮从周宿夜江游船码头到宁波大剧院游船码头顺流而行用40分钟，从宁波大剧院游船码头沿原线返回周宿夜江游船码头用了1小时，已知游轮在静水中的平均速度为8千米/小时，求水流的速度.设水流的速度为x千米/小时，则可列方程为( )

    A.40(8-x)=1×(8+x) B. (8+x)=8 C. (8+x)=8-x D.

    【答案】C

    【解析】

    设水流的速度为x千米/小时，则顺流航行的速度为（x+8）千米/小时，逆流航行的速度为（8-x）千米/小时，根据路程等于速度乘以时间得出两码头间的距离为 (8+x)千米或（8-x）千米，根据用两个不同的式子表示同一个量，则这两个式子应该相等，列出方程.

    解：设水流的速度为x千米/小时，则顺流航行的速度为（x+8）千米/小时，逆流航行的速度为（8-x）千米/小时，根据顺流航行与逆流航行的路程不变列出方程为： (8+x)=8-x.

    故答案为：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

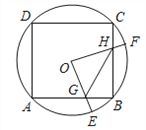
    【题目】如图，边长为4的正方形ABCD内接于⊙O，点E是上的一个动点(不与A、B重合)，点F是上的一点，连接OE、OF，分别与AB、BC交于点G、H，且∠EOF＝90°，有下列结论： ①； ②△OGH是等腰直角三角形； ③四边形OGBH的面积不随点E位置的变化而变化； ④△GBH周长的最小值为.其中错误的是______．(把你认为错误结论的序号填上)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校计划组织师生共300人参加一次大型公益活动，如果租用6辆大客车和5辆小客车，恰好全部坐满，已知每辆大客车的乘客座位数比小客车多17个．

    （1）求每辆大客车和每辆小客车的乘客座位数；

    （2）由于最后参加活动的人数增加了30人，学校决定调整租车方案，在保持租用车辆总数不变的情况下，且所有参加活动的师生都有座位，求租用小客车数量的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校七、八年级各有学生400人，为了解这两个年级普及安全教育的情况，进行了抽样调查，过程如下

    选择样本,收集数据从七、八年级各随机抽取20名学生,进行安全教育考试,测试成绩(百分制)如下：

    七年级 85 79 89 83 89 98 68 89 79 59

    99 87 85 89 97 86 89 90 89 77

    八年级 71 94 87 92 55 94 98 78 86 94

    62 99 94 51 88 97 94 98 85 91

    分组整理，描述数据

    (1)按如下频数分布直方图整理、描述这两组样本数据，请补全八年级20名学生安全教育频数分布直方图；

    (2)两组样本数据的平均数、中位数、众数、优秀率如下表所示，请补充完整；

    得出结论，说明理由.

    (3)整体成绩较好的年级为___,理由为___(至少从两个不同的角度说明合理性).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OA和OC是方程x(3+)x+3=0的两根(OA>OC),∠CAO=30°，将Rt△OAC折叠，使OC边落在AC边上，点O与点D重合，折痕为CE.

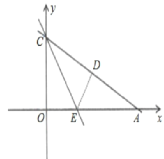
    (1)求点D的坐标；

    (2)设点M为直线CE上的一点,过点M作AC的平行线,交y轴于点N,是否存在这样的点M，使得以M、N、D. C为顶点的四边形是平行四边形?若存在，请求出符合条件的点M的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM+CN=10，则线段MN的长为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是甲、乙两车在某时段速度随时间变化的图像；下列说法：

    ①乙车前 4 秒行驶的路程为 48 米；

    ②在 0 到 8 秒内甲车的速度每秒增加 4 米；

    ③两车到第 3 秒时行驶的路程相等；

    ④在 4 到 8 秒内甲车的速度都大于乙车的速度.

    其中正确的有（ ）

    A. 1 个B. 2 个C. 3 个D. 4 个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某网店以每件80元的进价购进某种商品，原来按每件100元的售价出售，一天可售出50件;后经市场调查，发现这种商品每件的售价每降低2元，其销售量可增加10件.

    (1)该网店销售该商品原来一天可获利润 元.

    (2)设后来该商品每件售价降价元，网店一天可获利润元.

    ①若此网店为了尽可能增加该商品的销售量，且一天仍能获利1080元，则每件商品的售价应降价多少元?

    ②求与之间的函数关系式，当该商品每件售价为多少元时，该网店一天所获利润最大?并求最大利润值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为实施乡村振兴战略，解决某山区老百娃出行难的问题，当地政府决定修建一条高速公路，其中一段长为146米的山体隧道贯穿工程由甲、乙两个工程队负责施工，甲工程队独立工作2天后，乙工程队加入，两个工程队又联合工作了1天，这3天共掘进26米，已知甲工程队平均每天比乙工程队多掘进2米．

    （1）求甲、乙两个工程队平均每天分别掘进多少米？

    （2）若甲、乙两个工程队按此施工速度进行隧道贯穿工程，剩余工程由这两个工程队联合施工，求完成这项隧道贯穿工程一共需要多少天？

    查看答案和解析>>

    同步练习册答案