Question

15．△ABC是⊙O的内接三角形，AB=AC，点P是$\widehat{AB}$上一点，连接PA、PB、PC．
（1）如图1，若∠ABC=60°，求证：PA+PB=PC；
（2）如图2，点Q在$\widehat{AC}$上，且满足$\widehat{PQ}$=$\widehat{CQ}$，直线PA交BQ延长线于点H，求证：∠H=$\frac{1}{2}$∠BCP；
（3）如图3，在（2）的条件下，设BQ交PC于点M，若P为$\widehat{AB}$的中点，sin∠BPC=$\frac{24}{25}$，CM=24$\sqrt{10}$，求PM的长．

Answer 1

分析 （1）如图1中，在PC上截取一点M，使得PA=PM，连接AM．只要证明△PAB≌△MAC即可解决问题．
（2）如图2中，连接PQ、QC、AQ．只要证明△AQH≌△AQC，推出QC=HQ，∠H=∠ACQ，由此即可解决问题．
（3）如图3中，连接AO交BC于G，连接BO、PO，PQ、QC，OP交AB于N．由∠BPC=∠BOG，得sin∠BPC=sin∠BOG=$\frac{24}{25}$，设BG=24k，BO=25k，则OG=7k，求出PB，根据∠PBM=∠CBM，推出$\frac{PB}{BC}$=$\frac{PM}{CM}$，由此即可解决问题．

解答 （1）证明：如图1中，在PC上截取一点M，使得PA=PM，连接AM．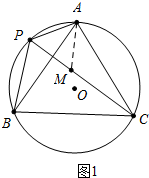

∵△ABC是等边三角形，
∴∠APC=∠ABC=60°，
∴△APM是等边三角形，
∴AP=AM，∠PAM=∠BAC=60°，
∴∠PAB=∠CAM，
在△PAB和△MAC中，
$\left\{\begin{array}{l}{AP=AM}\\{∠PAB=∠CAM}\\{AB=AC}\end{array}\right.$，
∴△PAB≌△MAC，
∴PB=CM，
∴PC=PM+CM=PA+PB．
∴PC=PA+PB．

（2）如图2中，连接PQ、QC、AQ．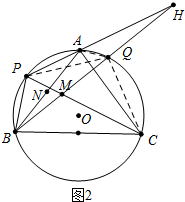

∵∠AQH+∠AQB=180°，∠AQC+∠ABC=180°，
又∵AB=AC，
∴∠ABC=∠ACB=∠AQB，
∴∠AQC=∠AQC，
∵∠HAQ=∠PBQ，
∵$\widehat{PQ}$=$\widehat{QC}$，
∴∠QAC=∠PBQ，
∴∠HAQ=∠CAQ，
在△QAH和△QAC中，
$\left\{\begin{array}{l}{∠HAQ=∠CAQ}\\{AQ=AQ}\\{∠AQH=∠AQC}\end{array}\right.$，
∴△AQH≌△AQC，
∴QC=HQ，∠H=∠ACQ，
∵∠ACQ=∠QPH=∠H，
∵∠PCB=∠PQB=∠QPH+∠H=2∠H，
∴∠H=$\frac{1}{2}$∠PCB．

（3）如图3中，连接AO交BC于G，连接BO、PO，PQ、QC，OP交AB于N．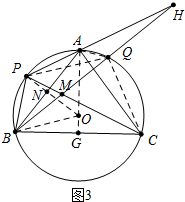

∵AB=AC，
∴$\widehat{AB}$=$\widehat{AC}$，
∴OA⊥BC，
∴∠BPC=∠BOG，
∴sin∠BPC=sin∠BOG=$\frac{24}{25}$，设BG=24k，BO=25k，则OG=7k，
∴AB=$\sqrt{B{G}^{2}+A{G}^{2}}$=40k，
在Rt△ANO中，ON=$\sqrt{O{A}^{2}-A{N}^{2}}$=15k，
∴PN=10k，PB=PA=$\sqrt{P{N}^{2}+A{N}^{2}}$=10$\sqrt{5}$k，
∵∠PBM=∠CBM，
∴$\frac{PB}{BC}$=$\frac{PM}{CM}$，
∴$\frac{10\sqrt{5}k}{48k}$=$\frac{PM}{24\sqrt{10}}$，
∴PM=25$\sqrt{2}$．

点评 本题考查圆综合题、全等三角形的判定和性质、勾股定理、角平分线的性质定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形，寻找全等三角形的条件是难点，属于中考压轴题．