
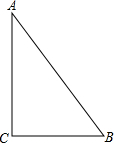
 如图,要在一块形状为直角三角形(∠C 为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮画出一个半圆,使它的圆心在线段AC 上,且与AB、BC 都相切.
如图,要在一块形状为直角三角形(∠C 为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮画出一个半圆,使它的圆心在线段AC 上,且与AB、BC 都相切.分析 (1)先确定圆心,再确定半径即可解决.
(2)利用S△ABC=S△BCO+S△ABO,列出方程即可解决.
解答 解:(1)作∠B的角平分线与AC的交点O,以O为圆心,OC为半径画半圆;
(2)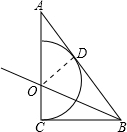 设半圆的半径为r,
设半圆的半径为r,
∵半圆O与AB相切于点D,
∴OD⊥AB,
∴∠ADO=90°
在Rt△ACB中,∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+C{B}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
在△ADO和△ACB中
∠ADO=∠ACB,∠A=∠A
∴△ADO∽△ACB
∴$\frac{AO}{AB}=\frac{OD}{BC}$
∴$\frac{4-r}{5}=\frac{r}{3}$,
解得:r=1.5.
答:半圆的半径为1.5.
点评 本题考查了切线的判断与性质、勾股定理以及相似三角形的判定与性质,此题综合性较强,比较复杂,一定要细心去做.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
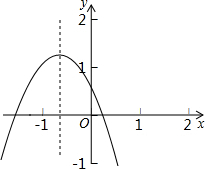 如图所示的二次函数y═ax2+bx+c的图象,下列结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0,其中正确的有( )
如图所示的二次函数y═ax2+bx+c的图象,下列结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=2 | D. | a=-1,b=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 cm | B. | 3 cm | C. | 17 cm | D. | 12 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com