
【题目】如图,已知点E,F分别是平行四边形ABCD的边BC,AD上的中点.
(1)AE与CF的关系是 ,请证明;
(2)若∠BAC= °时,四边形AECF是菱形,请说明理由.

【答案】(1)AE=CF,AE//CF,证明见解析;(2)90,理由见解析.
【解析】
(1)通过证明四边形AECF是平行四边形,可得AE=CF,AE//CF;
(2)由直角三角形的性质可得AE=CE,且四边形AECF是平行四边形,可得四边形AECF是菱形.
解:(1)AE=CF,AE//CF,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵点E,F分别是平行四边形ABCD的边BC,AD上的中点.
∴AF=CE,且AF∥CE,
∴四边形AECF是平行四边形,
∴AE=CF,AE//CF,
故答案为:AE=CF,AE//CF;
(2)90°,理由如下:
当∠BAC=90°时
∵点E是BC边的中点,
∴AE=CE=BE=![]() BC
BC
∵四边形AECF是平行四边形
∴平行四边形AECF是菱形.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
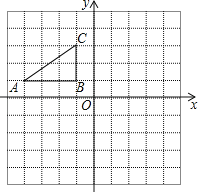
【题目】如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣4,1),B(﹣1,1),C(﹣1,3),请解答下列问题:
(1)画出△ABC关于原点O的中心对称图形△A1B1C1;
(2)画出△ABC关于y轴对称图形△A2B2C2,则△A2B2C2与△A1B1C1的位置关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期伊始,西大附中的学子们积极响应学校的“书香校园”活动,踊跃捐出自己喜爱的书籍,互相分享,让阅读成为一种习惯.据调查,某年级甲班、乙班共80人捐书,丙班有40人捐书,已知乙班人均捐书数量比甲班人均捐书数量多5本,而丙班的人均捐书数量是甲班人均捐书数量的一半,若该年级甲、乙、丙三班的人均捐书数量恰好是乙班人均捐书数量的![]() ,且各班人均捐书数量均为正整数,则甲、乙、丙三班共捐书_____本.
,且各班人均捐书数量均为正整数,则甲、乙、丙三班共捐书_____本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④![]() .其中一定成立的是( )
.其中一定成立的是( )

A.①②③B.②③④C.①③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年广东梅州11分)用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:

探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.
(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;
(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.
探究二:如图④,将△DEF的顶点D放在△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为测量某特种车辆的性能,研究制定了行驶指数![]() ,而
,而![]() 的大小与平均速度
的大小与平均速度![]() 和行驶路程
和行驶路程![]() 有关(不考虑其他因素),
有关(不考虑其他因素),![]() 由两部分的和组成,一部分与
由两部分的和组成,一部分与![]() 成正比,另一部分与
成正比,另一部分与![]() 成正比.在实验中得到了表格中的数据:
成正比.在实验中得到了表格中的数据:
速度 |
|
|
路程 |
|
|
指数 |
|
|
(1)用含![]() 和
和![]() 的式子表示
的式子表示![]() ;
;
(2)当行驶指数为![]() ,而行驶路程为
,而行驶路程为![]() 时,求平均速度的值;
时,求平均速度的值;
(3)当行驶路程为![]() 时,若行驶指数值最大,求平均速度的值.
时,若行驶指数值最大,求平均速度的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
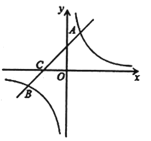
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)直接写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售为![]() 本,销售单价为
本,销售单价为![]() 元.
元.
(1)请直接写出![]() 与
与![]() 之间的函数关系式和自变量
之间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润![]() 元最大?最大利润是多少元?
元最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com