
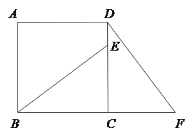
【题目】已知:如图,在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BEC≌△DFC;
(2)如果BC+DF=9,CF=3,求正方形ABCD的面积.
【答案】(1)证明见解析
(2)16
【解析】
试题(1)正方形的四个边相等,四个角都是直角,因此可得到BC=DC,∠ECD=∠FCD,由SAS可证明三角形全等.
(2)设BC=x,则CD=x,DF=9﹣x,CF=4,可用勾股定理求出x,因此可求出正方形ABCD的面积.
试题解析:(1)∵四边形ABCD是正方形
∴BC=CD,∠BCE=90°
∴∠DCF=180°-∠BCE=90°=∠BCE
在△BCE和△DCF中, ,
,
∴△BEC≌△DFC(SAS);
(2)设BC=x,则CD=x,DF=9﹣x,
在Rt△DCF中,CF=3,
∴CF2+CD2=DF2,
32+x2=(9﹣x)2,
解得x=4,正方形的面积为:4×4=16.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往![]() 县10辆,需要调往
县10辆,需要调往![]() 县8辆,已知从甲仓库调运一辆农用车到
县8辆,已知从甲仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为40元和80元;从乙仓库调运一辆农用车到
县的运费分别为40元和80元;从乙仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为30元和50元.
县的运费分别为30元和50元.
(1)设乙仓库调往![]() 县农用车
县农用车![]() 辆,求总运费
辆,求总运费![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若要求总运费不超过900元,问共有几种调运方案?试列举出来.
(3)求出总运费最低的调运方案,最低运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l所对应的函数表达式为y=x.过点A1(0,1)作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;过点A2作y轴的垂线交直线l于点B2 , 则点B2的坐标为( )

A. (1,1) B. (![]() ,
, ![]() ) C. (2,2) D. ( 2
) C. (2,2) D. ( 2![]() ,2
,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AB=BC=6,∠B=60°,∠D=90°,连结AC.动点P从点B出发,沿BC以每秒1个单位的速度向终点C运动(点P不与点B、C重合).过点P作PQ⊥BC交AB或AC于点Q,以PQ为斜边作Rt△PQR,使PR∥AB.设点P的运动时间为t秒.

(1)当点Q在线段AB上时,求线段PQ的长.(用含t的代数式表示)
(2)当点R落在线段AC上时,求t的值.
(3)设△PQR与△ABC重叠部分图形的面积为S平方单位,求S与t之间的函数关系式.
(4)当点R到C、D两点的距离相等时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.要测量学校一幢教学楼AB的高度如图所示,他们先在点C测得教学楼的顶部A的仰角为36.2°,然后向教学楼前进10米到达点D,又测得点A的仰角为45°.请你根据这些数据,求出这幢教学楼AB的高度.(结果精确到1米)
【参考数据:sin36.2°=0.59,cos36.2°=0.81,tan36.2°=0.73】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于A、B两点,动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,当其中一点到达终点时,另一点也随之停止运动.设点P运动的时间为t(秒).
轴分别交于A、B两点,动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,当其中一点到达终点时,另一点也随之停止运动.设点P运动的时间为t(秒).
(1)直接写出A、B两点的坐标.
(2)当△APQ与△AOB相似时,求t的值.
(3)设△APQ的面积为S(平方单位),求S与t之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
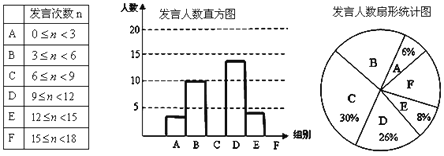
【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)样本容量是______________,并补全直方图;
(2)该年级共有学生800人,请估计该年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好都是男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在讲完乘法公式![]() 的多种运用后,要求同学们运用所学知识解答:求代数式
的多种运用后,要求同学们运用所学知识解答:求代数式![]() 的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
解:![]()
∵![]() ,
,
当![]() 时,
时,![]() 的值最小,最小值是0,
的值最小,最小值是0,
∴![]()
当![]() 时,
时,![]() 的值最小,最小值是1,
的值最小,最小值是1,
∴![]() 的最小值是1.
的最小值是1.
请你根据上述方法,解答下列各题
(1)当x=______时,代数式![]() 的最小值是______;
的最小值是______;
(2)若![]() ,当x=______时,y有最______值(填“大”或“小”),这个值是______;
,当x=______时,y有最______值(填“大”或“小”),这个值是______;
(3)若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在RtABC中,∠C=90°,AC=BC=![]() (如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为_____.
(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com