
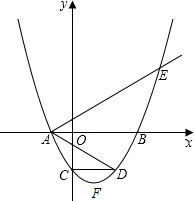
 ČēĶ¼£¬¶ž“ĪŗÆŹży=a£Øx2-4mx-12m2£©£ØĘäÖŠa£¬mŹĒ³£Źż£¬ĒŅa£¾0£¬m£¾0£©µÄĶ¼ĻóÓėxÖį·Ö±š½»ÓŚµćA”¢B£ØµćAĪ»ÓŚµćBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚC£Ø0£¬-6£©£¬µćDŌŚ¶ž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬CD”ĪAB£¬Į¬½ÓAD£¬¹żµćA×÷ÉäĻßAE½»¶ž“ĪŗÆŹżµÄĶ¼ĻóÓŚµćE£¬ABĘ½·Ö”ĻDAE£®
ČēĶ¼£¬¶ž“ĪŗÆŹży=a£Øx2-4mx-12m2£©£ØĘäÖŠa£¬mŹĒ³£Źż£¬ĒŅa£¾0£¬m£¾0£©µÄĶ¼ĻóÓėxÖį·Ö±š½»ÓŚµćA”¢B£ØµćAĪ»ÓŚµćBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚC£Ø0£¬-6£©£¬µćDŌŚ¶ž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬CD”ĪAB£¬Į¬½ÓAD£¬¹żµćA×÷ÉäĻßAE½»¶ž“ĪŗÆŹżµÄĶ¼ĻóÓŚµćE£¬ABĘ½·Ö”ĻDAE£®·ÖĪö £Ø1£©°ŃµćC×ų±ź“śČėy=a£Øx2-2mx-3m2£©ÖŠ£¬¼“æɽā¾öĪŹĢā£®
£Ø2£©ČēĶ¼1£¬¹żµćD”¢E·Ö±š×÷xÖįµÄ“¹Ļߣ¬“¹×ćĪŖM”¢N£®Ź×ĻČĒó³öA”¢BĮ½µć×ų±ź£¬ÓÉ”÷ADM”×”÷AEN£®ĶĘ³ö $\frac{AD}{AE}$=$\frac{AM}{AN}$=$\frac{DM}{EN}$£®ÉčE×ų±źĪŖ£Øx£¬$\frac{1}{{m}^{2}}$£Øx2-2mx-3m2£©£©£¬æÉµĆ $\frac{3}{\frac{1}{{m}^{2}}£Ø{x}^{2}-2mx-3{m}^{2}£©}$=$\frac{3m}{x-£Ø-m£©}$£¬ĶĘ³öx=4m£¬æɵĆE£Ø4m£¬5£©£¬ÓÉAM=AO+OM=m+2m=3m£¬AN=AO+ON=m+4m=5m£¬ÓÉ“Ė¼“æɽā¾öĪŹĢā£®
£Ø3£©ČēĶ¼2£¬¼Ē¶ž“ĪŗÆŹżĶ¼Ļ󶄵ćĪŖF£¬ŌņFµÄ×ų±źĪŖ£Øm£¬-4£©£¬¹żµćF×÷FH”ĶxÖįÓŚµćH£®Į¬½ÓFC²¢ŃÓ³¤£¬ÓėxÖįøŗ°ėÖį½»ÓŚŅ»µć£¬“Ėµć¼“ĪŖĖłĒóµÄµćG£®
ÓÉtan”ĻCGO=$\frac{OC}{OG}$£¬tan”ĻFGH=$\frac{HF}{HG}$£¬ĶĘ³ö $\frac{OC}{OG}$=$\frac{HF}{HG}$£¬ĶĘ³ö $\frac{OC}{OG}$=$\frac{HF}{OH+OG}$£¬ÓÉOC=3£¬HF=4£¬OH=m£¬æɵĆOG=3m£®ĶĘ³öGF=$\sqrt{G{H}^{2}+H{F}^{2}}$=$\sqrt{16{m}^{2}+16}$=4 $\sqrt{{m}^{2}+1}$£¬AD=$\sqrt{A{M}^{2}+M{D}^{2}}$=$\sqrt{9{m}^{2}+9}$=3 $\sqrt{{m}^{2}+1}$£¬æÉµĆ $\frac{GF}{AD}$=$\frac{4}{3}$£¬ÓÉ“Ė¼“æɽā¾öĪŹĢā£®
½ā“š £Ø1£©½ā£ŗ½«C£Ø0£¬-3£©“śČė¶ž“ĪŗÆŹży=a£Øx2-2mx-3m2£©£¬
Ōņ-3=a£Ø0-0-3m2£©£¬
½āµĆ a=$\frac{1}{{m}^{2}}$£®
£Ø2£©Ö¤Ć÷£ŗČēĶ¼1£¬¹żµćD”¢E·Ö±š×÷xÖįµÄ“¹Ļߣ¬“¹×ćĪŖM”¢N£®
ÓÉa£Øx2-2mx-3m2£©=0£¬
½āµĆ x1=-m£¬x2=3m£¬
Ōņ A£Ø-m£¬0£©£¬B£Ø3m£¬0£©£®
”ßCD”ĪAB£¬
”ąDµćµÄׯ×ų±źĪŖ-3£¬
ÓÖ”ßDµćŌŚÅ×ĪļĻßÉĻ£¬
”ą½«Dµćׯ×ų±ź“śČėÅ×ĪļĻß·½³ĢµĆDµćµÄ×ų±źĪŖ£Ø2m£¬-3£©£®
”ßABĘ½·Ö”ĻDAE£¬
”ą”ĻDAM=”ĻEAN£¬
”ß”ĻDMA=”ĻENA=90”ć£¬
”ą”÷ADM”×”÷AEN£®
”ą$\frac{AD}{AE}$=$\frac{AM}{AN}$=$\frac{DM}{EN}$£®
ÉčE×ų±źĪŖ£Øx£¬$\frac{1}{{m}^{2}}$£Øx2-2mx-3m2£©£©£¬
”ą$\frac{3}{\frac{1}{{m}^{2}}£Ø{x}^{2}-2mx-3{m}^{2}£©}$=$\frac{3m}{x-£Ø-m£©}$£¬
”ąx=4m£¬
”ąE£Ø4m£¬5£©£¬
”ßAM=AO+OM=m+2m=3m£¬AN=AO+ON=m+4m=5m£¬
”ą$\frac{AD}{AE}$=$\frac{AM}{AN}$=$\frac{3}{5}$£¬¼“ĪŖ¶ØÖµ£®
£Ø3£©½ā£ŗČēĶ¼2£¬¼Ē¶ž“ĪŗÆŹżĶ¼Ļ󶄵ćĪŖF£¬ŌņFµÄ×ų±źĪŖ£Øm£¬-4£©£¬¹żµćF×÷FH”ĶxÖįÓŚµćH£®
Į¬½ÓFC²¢ŃÓ³¤£¬ÓėxÖįøŗ°ėÖį½»ÓŚŅ»µć£¬“Ėµć¼“ĪŖĖłĒóµÄµćG£®
”ßtan”ĻCGO=$\frac{OC}{OG}$£¬tan”ĻFGH=$\frac{HF}{HG}$£¬
”ą$\frac{OC}{OG}$=$\frac{HF}{HG}$£¬
”ą$\frac{OC}{OG}$=$\frac{HF}{OH+OG}$£¬
”ßOC=3£¬HF=4£¬OH=m£¬
”ąOG=3m£®
”ßGF=$\sqrt{G{H}^{2}+H{F}^{2}}$=$\sqrt{16{m}^{2}+16}$=4 $\sqrt{{m}^{2}+1}$£¬
AD=$\sqrt{A{M}^{2}+M{D}^{2}}$=$\sqrt{9{m}^{2}+9}$=3 $\sqrt{{m}^{2}+1}$£¬
”ą$\frac{GF}{AD}$=$\frac{4}{3}$£®
”ß$\frac{AD}{AE}$=$\frac{3}{5}$£¬
”ąAD£ŗGF£ŗAE=3£ŗ4£ŗ5£¬
”ąŅŌĻ߶ĪGF£¬AD£¬AEµÄ³¤¶ČĪŖČż±ß³¤µÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ£®
µćĘĄ ±¾Ģāæ¼²éĮĖ¶ž“ĪŗÆŹż×ŪŗĻĢā”¢¹“¹É¶ØĄķ”¢¹“¹É¶ØĄķµÄÄę¶ØĄķ”¢½ĒĘ½·ÖĻߵĶØŅ唢Čń½ĒČż½ĒŗÆŹż”¢²ĪŹżŹĒ¾ŲŠĪµÄÅŠ¶ØŗĶŠŌÖŹµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒĮé»īŌĖÓĆĖłŃ§ÖŖŹ¶½ā¾öĪŹĢā£¬Ń§»įĄūÓĆ²ĪŹż½ā¾öĪŹĢā£¬ŹōÓŚÖŠæ¼Ń¹ÖįĢā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | øŗŹż | B£® | ·ĒÕżŹż | C£® | ÕżŹż | D£® | ²»ÄÜČ·¶Ø |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com