
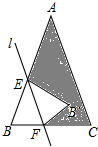
 等腰三角形ABC中,顶角A是大于0°小于180°的任意角,直接l∥AC并AB于E,交BC于F,沿直线l折叠角B,点B的对应点为B′,请对以下结论做出判断:
等腰三角形ABC中,顶角A是大于0°小于180°的任意角,直接l∥AC并AB于E,交BC于F,沿直线l折叠角B,点B的对应点为B′,请对以下结论做出判断:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据等腰三角形和平行线的性质即可得到△EBF是等腰三角形;故①正确;根据折叠的性质得到EB′=EB,FB′=FB,于是得到阴影部分图形的周长=AE+EB′+FB′+FC+AC=AE+BE+BF+CF+AC=AB+BC+AC=△ABC的周长;故②正确;由∠B=70°,得到∠EFB=∠EFB′=70°,∠BEF=∠FEB′=40°,于是得到∠AEB′=100°,得到③正确;由∠B=20°,于是得到∠EFB=∠EFB′=20°,得到∠CFB′=140°,推出∠CFB′+∠AEB′>140°故④错误.
解答 解:∵AB=AC,
∴∠B=∠C,
∴EF∥AC,
∴∠EFB=∠C,
∴∠EFB=∠B,
∴①△EBF一定是等腰三角形;故①正确;
∵直线l折叠角B,点B的对应点为B′,
∴EB′=EB,FB′=FB,
∴阴影部分图形的周长=AE+EB′+FB′+FC+AC=AE+BE+BF+CF+AC=AB+BC+AC=△ABC的周长;故②正确;
∵∠B=70°,
∴∠EFB=∠EFB′=70°,∠BEF=∠FEB′=40°,
∴∠AEB′=100°,
∴∠CFB′+∠AEB′=140°,故③正确;
∵∠B=20°,
∴∠EFB=∠EFB′=20°,
∴∠CFB′=140°,
∴∠CFB′+∠AEB′>140°,故④错误;
故选C.
点评 本题考查了翻折变换-折叠问题,等腰三角形的判定和性质,熟练掌握折叠的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
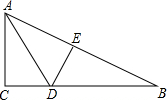 如图,有一块直角三角形纸片,两直角边AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为( )
如图,有一块直角三角形纸片,两直角边AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
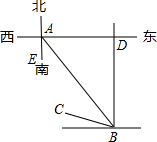 如图,小张从家(图中A处)出发,向南偏东40°的方向走到学校(图中B处)再从学校出发,向北偏西75°的方向走到小明家(图中C处),则∠ABC为35度.
如图,小张从家(图中A处)出发,向南偏东40°的方向走到学校(图中B处)再从学校出发,向北偏西75°的方向走到小明家(图中C处),则∠ABC为35度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
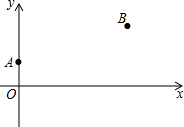 如图所示,A,B两村在某条河的同侧,以河岸为x轴,建立直角坐标系,A,B两村相对应的坐标为(0,1),(4,2)(长度单位为km).现在要在河岸的P点处直接向A,B两村送水,则点P选在何处才能使所用的水管最短?试写出点P的坐标及所需水管的长度.
如图所示,A,B两村在某条河的同侧,以河岸为x轴,建立直角坐标系,A,B两村相对应的坐标为(0,1),(4,2)(长度单位为km).现在要在河岸的P点处直接向A,B两村送水,则点P选在何处才能使所用的水管最短?试写出点P的坐标及所需水管的长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com