
【题目】在平面直角坐标系![]() 中,
中,![]() 为抛物线
为抛物线![]() 上任意两点,其中
上任意两点,其中![]() .
.
(1)若抛物线的对称轴为![]() ,当
,当![]() 为何值时,
为何值时,![]()
(2)设抛物线的对称轴为![]() .若对于
.若对于![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据抛物线解析式得抛物线必过(0,c),因为![]() ,抛物线的对称轴为
,抛物线的对称轴为![]() ,可得点M,N关于
,可得点M,N关于![]() 对称,从而得到
对称,从而得到![]() 的值;
的值;
(2)根据题意知,抛物线开口向上,对称轴为![]() ,分3种情况讨论,情况1:当
,分3种情况讨论,情况1:当![]() 都位于对称轴右侧时,情况2:当
都位于对称轴右侧时,情况2:当![]() 都位于对称轴左侧时,情况3:当
都位于对称轴左侧时,情况3:当![]() 位于对称轴两侧时,分别求出对应的t值,再进行总结即可.
位于对称轴两侧时,分别求出对应的t值,再进行总结即可.
解:(1)当x=0时,y=c,
即抛物线必过(0,c),
∵![]() ,抛物线的对称轴为
,抛物线的对称轴为![]() ,
,
∴点M,N关于![]() 对称,
对称,
又∵![]() ,
,
∴![]() ,
,![]() ;
;
(2)由题意知,a>0,
∴抛物线开口向上
∵抛物线的对称轴为![]() ,
,![]()
∴情况1:当![]() 都位于对称轴右侧时,即当
都位于对称轴右侧时,即当![]() 时,
时,![]() 恒成立
恒成立
情况2:当![]() 都位于对称轴左侧时,即
都位于对称轴左侧时,即![]() <
<![]() 时,
时,![]() 恒不成立
恒不成立
情况3:当![]() 位于对称轴两侧时,即当
位于对称轴两侧时,即当![]()
![]() 时,要使
时,要使![]() ,必有
,必有![]() ,即
,即![]()
解得![]() ,
,
∴3≥2t,
∴![]()
综上所述,![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
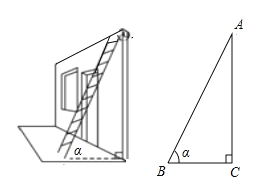
【题目】如图.要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角![]() 一般要满足
一般要满足![]() ,现有一架长
,现有一架长![]() 的梯子.
的梯子.
(1)使用这架梯子最高可以安全攀上多高的墙(结果保留小数点后一位)?
(2)当梯子底端距离墙面![]() 时,
时,![]() 等于多少度(结果保留小数点后一位)?此时人是否能够安全使用这架梯子?
等于多少度(结果保留小数点后一位)?此时人是否能够安全使用这架梯子?
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了美化环境,计划分两次购进A,B两种花,第一次分别购进A,B两种花30棵和15棵,共花费675元;第二次以同样的单价分别购进A、B两种花12棵和5棵,第二次花费265元.
(1)求A、B两种花的单价分别是多少元?
(2)若购买A、B两种花共31棵,且B种花的数量不多于A种花的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点E为□ABCD对角线AC上的一点,点F在线段BE的延长线上,且EF=BE,线段EF与边CD相交于点G.
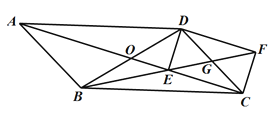
(1)求证:DF//AC;
(2)如果AB=BE,DG=CG,联结DE、CF,求证:四边形DECF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
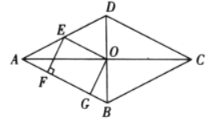
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
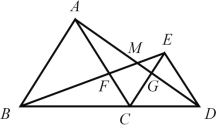
【题目】如图所示,![]() 均为等边三角形,边长分别为
均为等边三角形,边长分别为![]() ,B、C、D三点在同一条直线上,则下列结论正确的________________.(填序号)
,B、C、D三点在同一条直线上,则下列结论正确的________________.(填序号)
①![]() ②
②![]() ③
③![]() 为等边三角形 ④
为等边三角形 ④![]() ⑤CM平分
⑤CM平分![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴,y轴交于点A,B两点,点C为OB的中点,抛物线
分别与x轴,y轴交于点A,B两点,点C为OB的中点,抛物线![]() 经过A,C两点.
经过A,C两点.

(1)求抛物线的函数表达式;
(2)点D是直线AB下方的抛物线上的一点,且![]() 的面积为
的面积为![]() ,求点D的坐标;
,求点D的坐标;
(3)点P为抛物线上一点,若![]() 是以AB为直角边的直角三角形,求点P到抛物线的对称轴的距离.
是以AB为直角边的直角三角形,求点P到抛物线的对称轴的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
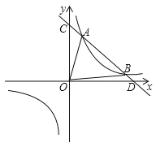
【题目】如图,已知一次函数y1=﹣x+a与x轴、y轴分别交于点D、C两点和反比例函数![]() 交于A、B两点,且点A的坐标是(1,3),点B的坐标是(3,m)
交于A、B两点,且点A的坐标是(1,3),点B的坐标是(3,m)
(1)求a,k,m的值;
(2)求C、D两点的坐标,并求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送.若两车合作,各运12趟才能完成,需支付运费共4800元;若甲、乙两车单独运完此堆垃圾,则乙车所运趟数是甲车的2倍;已知乙车每趟运费比甲车少200元.
探究:
(1)分别求出甲、乙两车每趟的运费;
(2)若单独租用甲车运完此堆垃圾,需运多少趟;
发现:若同时租用甲、乙两车,则甲车运x趟,乙车运y趟,才能运完此堆垃圾,其中![]() 均为正整数.
均为正整数.
(1)当![]() 时,
时,![]() ______;当
______;当![]() 时,
时,![]() ______;
______;
(2)求y与x之间满足的函数关系式.
决策:在“发现”的条件下,设总运费为w(元).
(1)求w与x之间满足的函数关系式,当x取何值时,w取得最小值;
(2)当![]() 且
且![]() 时,甲车每趟的运费打7折,乙车每趟的运费打9折,当x取何值时,w取得最小值.
时,甲车每趟的运费打7折,乙车每趟的运费打9折,当x取何值时,w取得最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com