
【题目】在平面直角坐标系xOy中,抛物线y=mx2-2m2x+2交y轴于点A,交直线x=4于点B.
(1)抛物线的对称轴为x=____________(用含m的代数式表示)
(2)若AB∥x轴,求抛物线的解析式.
(3)记抛物线在A、B之间的部分为图象G(包含A、B两点),若对于图象G上任意一点P(xp,yp),都有yp≤2,求m的取值范围.
【答案】(1)m(2)y=2x2-8x+2(3)m<0或m≥2
【解析】
(1)根据抛物线的对称轴为直线x=-![]() ,代入数据即可得出结论;
,代入数据即可得出结论;
(2)由AB∥x轴,可得出点B的坐标,进而可得出抛物线的对称轴为x=2,结合(1)可得出m=2,将其代入抛物线表达式中即可;
(3)分m>0及m<0两种情况考虑,依照题意画出函数图象,利用数形结合即可得出m的取值范围.
解:(1)抛物线的对称轴为![]()
故答案为:m.
(2)当x=0时,y=mx2-2m2x+2=2,
∴点A(0,2).
∵AB∥x轴,且点B在直线x=4上,
∴点B(4,2),抛物线的对称轴为直线x=2,
∴m=2,
∴抛物线的表达式为y=2x2-8x+2.
(3)当m>0时,如图1.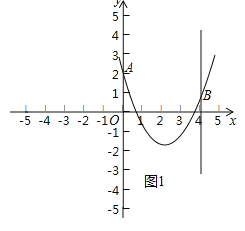
∵A(0,2),
∴要使0≤xp≤4时,始终满足yp≤2,只需使抛物线y=mx2-2m2x+2的对称轴与直线x=2重合或在直线x=2的右侧.
∴m≥2;
当m<0时,如图2,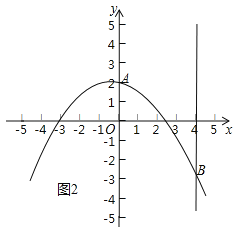
在0≤xp≤4中,yp≤2恒成立.
综上所述,m的取值范围为m<0或m≥2.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,且
的直径,且![]() ,
,![]() 是
是![]() 上一点,将弧
上一点,将弧![]() 沿直线
沿直线![]() 翻折,若翻折后的圆弧恰好经过点
翻折,若翻折后的圆弧恰好经过点![]() ,取
,取![]() ,
,![]() ,
,![]() ,那么由线段
,那么由线段![]() 、
、![]() 和弧
和弧![]() 所围成的曲边三角形的面积与下列四个数值最接近的是( )
所围成的曲边三角形的面积与下列四个数值最接近的是( )
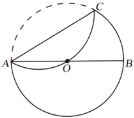
A.3.2B.3.6C.3.8D.4.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是一个晾衣架的实物图,支架的基本图形是菱形,MN是晾衣架的一个滑槽,点P在滑槽MN上,下移动时,晾衣架可以伸缩,其示意图如图(2)所示,已知每个菱形的边长均为![]() ,且
,且![]() .(点D是固定点)
.(点D是固定点)

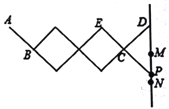
(1)当点P向下滑至点N处时,测得![]() 时
时
①求滑槽MV的长度
②此时点A到直线DP的距离是多少?
(2)当点P向上滑至点M处时,点A在相对于(1)的情况下向左移动的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,下列结论:
,下列结论:
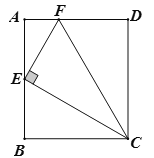
①![]() ;
;
②![]() ;
;
③![]() ;
;
④若![]() ,则
,则![]() .
.
其中正确的结论是______________.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=-x与函数y=-![]() 的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为____________.
的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为____________.
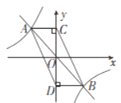
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数上的定点是指,一个含参数的函数无论参数取何值,函数的图象都过某一个点,这个点称为定点.例如,在函数y=kx中,当x=0时,无论参数k取何值,函数值y=0,所以这个函数过定点(0,0).
(1)分别求函数y=kx+2k和y=kx2﹣kx+2019的定点;
(2)若过原点的两条直线OA、OB分别与二次函数y=![]() x2交于点A(m,
x2交于点A(m,![]() m2)和点B(n,
m2)和点B(n,![]() n2)(mn<0)且OA⊥OB,试求直线AB上的定点;
n2)(mn<0)且OA⊥OB,试求直线AB上的定点;
(3)若直线CD:y=kx+2k+5与抛物线y=x2交于C、D两点,试在抛物线y=x2上找一定点E,使∠CED=90°,求点E的坐标,并求出点E到直线CD的最大距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位数字与百位数字之和为x,十位数字与个位数字之和为y,如果x=y,那么称这个四位数为“平衡数”.
(1)最小的“平衡数”为 ;四位数A与4738之和为最大的“平衡数”,则A的值为 ;
(2)一个四位“平衡数”M,它的个位数字是千位数字a的3倍,百位数字与十位数字之和为8,且千位数字a使得二次函数y=(a﹣2)x2﹣(2a﹣3)x+a﹣3与x轴有两个交点,求出所有满足条件的“平衡数”M的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
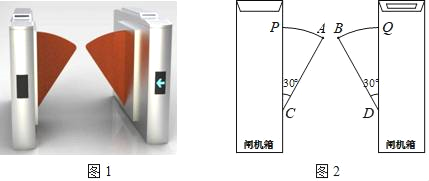
A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com