Question

阅读理解，填写部分理由，探索新的结论（②③两小题只写结论）
已知AB∥CD，①如图，∠B+∠C=∠BEC．

理由如下：
解：过E点作EF∥AB
则∠1=∠B（________）
∵EF∥AB
AB∥CD（________）
∴EF∥CD（________）
∴∠2=∠C（________）
∵∠BEC=∠1+∠2
∴∠BEC=∠C+∠B（________）
②图乙中∠B，∠E，∠D，∠F，∠C的数量关系是________；
③图丙中∠B，∠E，∠F，∠G，∠H，∠M，∠C的数量关系是________．

Answer 1

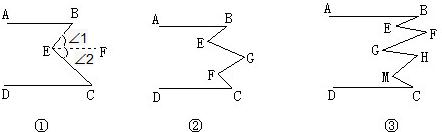
两直线平行内错角相等    已知    如果两条直线都与第三条直线平行，那么这两条直线也互相平行    两直线平行内错角相等    等量代换    ∠B+∠G+∠C=∠E+∠F    ∠B+∠F+∠H+∠C=∠E+∠G+∠M
分析：（1）利用平行线的性质和判定填空即可．
（2）（3），与（1）同理，只不过多了几条平行线，首先也要添加辅助线，然后利用平行线的性质和判定填空即可．
解答：
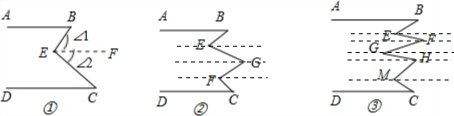
①过E点作EF∥AB，
则∠1=∠B（ 两直线平行内错角相等）
∵EF∥AB，
AB∥CD（ 已知）
∴EF∥CD（ 如果两条直线都与第三条直线平行，那么这两条直线也互相平行）
∴∠2=∠C（ 两直线平行内错角相等）
∵∠BEC=∠1+∠2，
∴∠BEC=∠C+∠B（ 等量代换）
②图乙中∠B，∠E，∠D，∠F，∠C的数量关系是∠B+∠G+∠C=∠E+∠F；
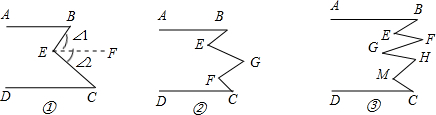
证明：过E、F、G作EH∥AB，GM∥AB，FN∥AB，
∵AB∥CD，
∴AB∥EH∥MG∥FN∥CD，
∴∠B=∠BEH，∠HEG=∠EGM，∠MGF=∠GFN，∠NFC=∠C，
∵∠BEG=∠BEH+∠HEG，∠EGF=∠EGM+∠MGF，∠GFC=∠GFN+∠NFC，
∴∠B+∠G+∠C=∠E+∠F；
③图丙中∠B，∠E，∠F，∠G，∠H，∠M，∠C的数量关系是∠B+∠F+∠H+∠C=∠E+∠G+∠M．
证明：过E、F、G、H、M作EK∥AB，FN∥AB，GP∥AB，HQ∥AB，MI∥AB，
∵AB∥CD，
∴AB∥EK∥FN∥GP∥HQ∥MI∥CD，
∴∠B=∠BEK，∠EFN=∠FGP，∠PGH=∠GHQ，∠QHM=∠HMI，∠IMC=∠C，
∵∠BEF=∠BEK+∠KEF，∠EFG=∠EFN+∠NFG，∠FGH=∠FGP+∠PGH，∠GHM=∠GHQ+∠QHM，∠HMC=∠HMI+∠IMC，
∴∠B+∠F+∠H+∠C=∠E+∠G+∠M．
点评：本题主要考查了平行线的判定和性质，但在作本题时，作出平行线是关键．