
分析 (1)利用二次函数平移的性质得出平以前的函数解析式;
(2)利用配方法求出二次函数的顶点坐标;
(3)根据勾股定理求得即可.
解答 解:(1)∵y=x2+bx+c的图象向右平移2个单位,再向下平移3个单位,得到图象的解析式为y=x2-2x-3,
∴y=x2-2x-3=(x-1)2-4,向左平移2个单位,向上平移3个单位后得到:y=(x+1)2-1=x2+2x,
故b=2,c=0;
故答案为2,0;
(2)由(1)得:原函数图象的顶点坐标为:(-1,-1);
(3)由y=x2-2x-3=(x-1)2-4可知平移后的顶点(1,-4),
∵原函数图象的顶点坐标为:(-1,-1);,
∴两个图象顶点之间的距离=$\sqrt{(1+1)^{2}+(-4+1)^{2}}$=$\sqrt{13}$.
点评 此题主要考查了二次函数图象与几何变换,正确掌握配方法求二次函数顶点坐标是解题关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
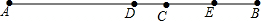 已知(如图),点C是线段AB上的一点,3AC=2AB,AD=$\frac{1}{2}$AB,CB:CE=2:1,DE=6,求AB的长度?
已知(如图),点C是线段AB上的一点,3AC=2AB,AD=$\frac{1}{2}$AB,CB:CE=2:1,DE=6,求AB的长度?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
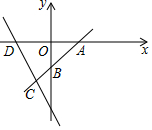 已知直线l1经过点A(2,0)和B(0,-2),直线l2:y=-$\frac{1}{2}$x-5与l1相交于点C,与x轴的交点D.
已知直线l1经过点A(2,0)和B(0,-2),直线l2:y=-$\frac{1}{2}$x-5与l1相交于点C,与x轴的交点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com