
(本小题满分8分)如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A在y轴上,点C在x轴上,且![]() ,OB=OC.
,OB=OC.
(1)求点B的坐标;
(2)点P从C点出发,沿线段CO以5个单位/秒的速度向终点O匀速运动,过点P作PH⊥OB,垂足为H,设△HBP的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,过点P作PM∥CB交线段AB于点M,过点M作MR⊥OC,垂足为R,线段MR分别交直线PH、OB于点E、G,点F为线段PM的中点,联结EF.
①判断EF与PM的位置关系;
②当t为何值时,![]() ?
?
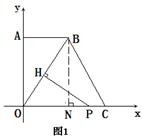
解:(1)如图1,过点B作BN⊥OC,垂足为N
 ∵
∵![]() ,OB=OC
,OB=OC
∴OA=8,OC=10 -------------------------------1分
∴OB=OC=10, BN=OA=8
∴![]()
∴B (6,8) ----------------------------------------------2分
(2)如图1,∵∠BON=∠POH,∠ONB=∠OHP=90°.
∴△BON∽△POH ∴![]()
∵PC=5t. ∴OP=10-5t. ∴OH=6-3t. PH=8-4t.
∴BH=OB-OH=10-(6-3t)=3t+4
∴![]() ------------------------------------ 3分
------------------------------------ 3分
∴t的取值范围是:0≤t<2 ------------------------------------------4分
(3)①EF⊥PM ----------------------------------------------------5分
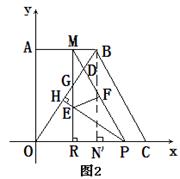 ∵MR⊥OC,PH⊥OB
∵MR⊥OC,PH⊥OB
∴∠RPM+∠RMP=90°,∠HPD+∠HDP=90°
∵OC=OB ∴∠OCB=∠OBC.
∵BC∥PM
∴∠RPM=∠HDP,∴∠RMP=∠HPD,即:∠ EMP=∠HPM
∴EM=EP
∵点F为PM的中点 ∴EF⊥PM ----------6分
②如图2过点B作BN′⊥OC,垂足为 N′,BN′=8,CN′=4
∵BC∥PM,MR⊥OC
∴△MRP≌△B N′C
∴PR=C N′=4
设EM=x,则EP=x
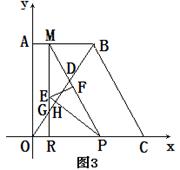 在△PER中,∠ERP=90°,RE=MR-ME=8-x
在△PER中,∠ERP=90°,RE=MR-ME=8-x
有![]() ,∴x=5
,∴x=5
∴ME=5
∵△MGB∽△N′BO
∴![]()
∵ PM∥CB,AB∥OC
∴四边形BMPC是平行四边形. ∴ BM=PC=5t.
第一种情况:当点G在点E上方时(如图2)
∵EG=2,∴MG=EM-EG=5-2=3
∴![]() ∴t=
∴t=![]() --------------------7分
--------------------7分
第二种情况:当点G在点E下方时(如图3) MG=ME+EG=5+2=7,
∴![]() ,∴t=
,∴t=![]() -------------------------------------------8分
-------------------------------------------8分
∴当t=![]() 或
或![]() 时,
时,![]() .
.
解析:略


科目:初中数学 来源: 题型:
(本小题满分7分)
如图,已知抛物线y1=-x2+bx+c经过A(1,0),B(0,-2)两点,顶点为D.

1.(1)求抛物线y1 的解析式;
2.(2)将△AOB绕点A逆时针旋转90°后,得到△AO′ B′ ,将抛物线y1沿对称轴平移后经过点B′ ,写出平移后所得的抛物线y2 的解析式;
3.(3)设(2)的抛物线y2与![]() 轴的交点为B1,顶点为D1,若点M在抛物线y2上,且满足△MBB1的面积是△MDD1面积的2倍,求点M的坐标.
轴的交点为B1,顶点为D1,若点M在抛物线y2上,且满足△MBB1的面积是△MDD1面积的2倍,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
(本小题满分6分)
如图,在8×11的方格纸中,每个小正方形的边长均为1,△ABC的顶点均在小正方形的顶点处.

1.(1)画出△ABC绕点A顺时针方向旋转90°得到的△![]() ;
;
2.(2)求点B运动到点B′所经过的路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
(本小题满分14分)
如图1,抛物线![]() 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线![]() 与抛物线交于点B、C.
与抛物线交于点B、C.

1.(1)求点A的坐标;
2.(2)当b=0时(如图2),求![]() 与
与![]() 的面积。
的面积。
3.(3)当![]() 时,
时,![]() 与
与![]() 的面积大小关系如何?为什么?
的面积大小关系如何?为什么?
4.(4)是否存在这样的b,使得![]() 是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2010-2011年江苏省常州实验初级中学九年级第二学期模拟考试数学卷 题型:解答题
(本小题满分8分)如图所示的矩形包书纸中,虚线是折痕,阴影是裁剪掉的部分,四个角均为大小相同的正方形,正方形的边长为折叠进去的宽度.
【小题1】(1)设课本的长为a cm,宽为b cm,厚为c cm,如果按如图所示的包书方式,将封面和封底 各折进去3cm,用含a,b,c的代数式,分别表示满足要求的矩形包书纸的长与宽;
【小题2】(2)现有一本长为19cm,宽为16cm,厚为6cm的字典,你能用一张长为43cm,宽为26cm的矩形纸包好这本字典,并使折叠进去的宽度 不小于3cm吗?请说明理由.
不小于3cm吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年河北省石家庄市42中学九年级第一次模拟考试数学卷 题型:解答题
(本小题满分9分) 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的
如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的 ,另一根露出水面的长度是它的
,另一根露出水面的长度是它的 .两根铁棒长度之和为55 cm.
.两根铁棒长度之和为55 cm.
(1)根据题意,甲、乙两个同学分别列出了尚不完整的方程(组)如下:
 甲:
甲: 乙:
乙: =55
=55
根据甲、乙两名同学所列的方程(组),请你分别指出未知数x,y表示的意义,然后在横线上补全甲、乙两名同学所列的方程(组):
甲:x表示 ,y表示 ;
乙:x表示 ;
(2)求此时木桶中水的深度多少cm?(写出完整的解答过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com