
���� ��1�����ݲ�����ɵ÷����ļ�����
��2�����ݲ�����ɵ÷����ļ�����
��3�����ݲ�����ɵ÷����ļ���..
��� �⣺��1��$\frac{1}{1��2}$+$\frac{1}{2��3}$+$\frac{1}{3��4}$+��+$\frac{1}{2014��2015}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+��+$\frac{1}{2014}$-$\frac{1}{2015}$=1-$\frac{1}{2015}$=$\frac{2014}{2015}$��
��2��$\frac{1}{1��2}$+$\frac{1}{2��3}$+$\frac{1}{3��4}$+��+$\frac{1}{n��n+1��}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+��+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{1+n}$=$\frac{n}{n+1}$��
��3��$\frac{1}{1��3}$+$\frac{1}{3��5}$+$\frac{1}{5��7}$+��+$\frac{1}{��2n-1����2n+1��}$=$\frac{17}{35}$��
$\frac{1}{2}$����1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+��+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$��=$\frac{17}{35}$��
1-$\frac{1}{2n+1}$=$\frac{34}{35}$��
$\frac{2n}{2n+1}$=$\frac{34}{35}$��
���n=17��
���� ���⿼���˷�ʽ�ļӼ���������ó���Ϊ�෴������������ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
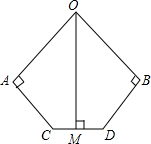 ��ͼ��OA=0B��AC=BD��0A��AC��0B��BD��OM��CD��M����֤��OMƽ�֡�A0B��
��ͼ��OA=0B��AC=BD��0A��AC��0B��BD��OM��CD��M����֤��OMƽ�֡�A0B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com