
【题目】已知顶点为P的抛物线C1的解析式为y=a(x-3)2(a≠0),且经过点(0,1).
(1)求a的值及抛物线C1的解析式;
(2)如图,将抛物线C1向下平移h(h>0)个单位得到抛物线C2,过点K(0,m2)(m>0)作直线l平行于x轴,与两抛物线从左到右分别相交于A,B,C,D四点,且A,C两点关于y轴对称.
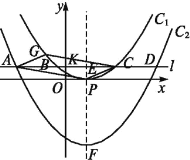
①点G在抛物线C1上,当m为何值时,四边形APCG为平行四边形?
②若抛物线C1的对称轴与直线l交于点E,与抛物线C2交于点F.试探究:在K点运动过程中,![]() 的值是否改变?若会,请说明理由;若不会,请求出这个值.
的值是否改变?若会,请说明理由;若不会,请求出这个值.
【答案】(1)y=![]() (x-3)2(2)①当m=
(x-3)2(2)①当m=![]() 时,四边形APCG是平行四边形②
时,四边形APCG是平行四边形②![]()
【解析】
(1)直接利用待定系数法求二次函数解析式得出即可;
(2)首先得出△GQK≌△POK(ASA),进而得出顶点G在抛物线C1上,得出2m2=![]() (-3-3)2,进而得出答案;
(-3-3)2,进而得出答案;
(3)利用函数对称性表示出A点坐标,再表示出KC,PF的长,进而得出其比值.
(1)∵抛物线C1过点(0,1),∴1=a(0-3)2,解得a=![]()
∴抛物线C1的解析式为y=![]() (x-3)2.
(x-3)2.
(2)①连接PG,∵点A,C关于y轴对称,
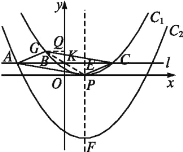
∴点K为AC的中点.
若四边形APCG是平行四边形,则必有点K是PG的中点.
过点G作GQ⊥y轴于点Q,
可得△GQK≌△POK,
∴GQ=PO=3,KQ=OK=m2,OQ=2m2.
∴点G(-3,2m2).
∵顶点G在抛物线C1上,∴2m2=![]() (-3-3)2,
(-3-3)2,
解得m=±![]() ,又m>0,∴m=
,又m>0,∴m=![]()
∴当m=![]() 时,四边形APCG是平行四边形.
时,四边形APCG是平行四边形.
②不会.在抛物线y=![]() (x-3)2中,令y=m2,
(x-3)2中,令y=m2,
解得x=3±3m,又m>0,且点C在点B的右侧,
∴C(3+3m,m2),KC=3+3m.
∵点A,C关于y轴对称,
∴A(-3-3m,m2).
∵抛物线C1向下平移h(h>0)个单位得到抛物线C2,∴抛物线C2的解析式为y=![]() (x-3)2-h.
(x-3)2-h.
∴m2=![]() (-3-3m-3)2-h,
(-3-3m-3)2-h,
解得h=4m+4,
∴PF=4+4m.
![]() .
.


科目:初中数学 来源: 题型:
【题目】我市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资![]() (吨)与时间
(吨)与时间![]() (小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
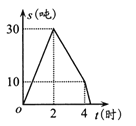
A. 4小时B. 4.3小时C. 4.4小时D. 5小时
查看答案和解析>>
科目:初中数学 来源: 题型:
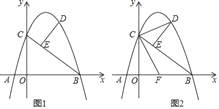
【题目】如图,A(﹣1,0),B(4,0),C(0,3)三点在抛物线y=ax2+bx+c上,D为直线BC上方抛物线上一动点,E在CB上,∠DEC=90°
(1)求抛物线的函数表达式;
(2)如图1,求线段DE长度的最大值;
(3)如图2,F为AB的中点,连接CF,CD,当△CDE中有一个角与∠CFO相等时,求点D的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
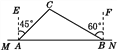
(1)MN是否穿过原始森林保护区?为什么?(参考数据: ![]() ≈1.732)
≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育节中,学校组织八年级学生举行定点投篮比赛,要求每班选派10名队员参加.下面是一班和二班参加队员定点投篮比赛成绩的折线统计图(每人投篮10次,每投中一次记1分),请根据图中信息回答下列问题:
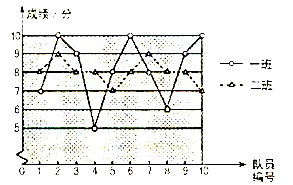
(1)将下表中一、二班队员投篮比赛成绩的有关数据补充完整:

(2)观察统计图,判断一班、二班10名队员投篮成绩的方差的大小关系:S2一班 S2二班;
(3)综合(1)(2)中的数据,选择一个方面对一班、二班10名队员定点投篮比赛成绩进行评价.
例如:从两班成绩的平均数看,一班成绩高于二班,除此之外,你的评价是:
查看答案和解析>>
科目:初中数学 来源: 题型:
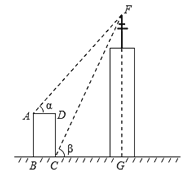
【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为∠α=48°和∠β=65°,矩形建筑物宽度AD=20m,高度CD=30m,则信号发射塔顶端到地面的高度FG为__米(结果精确到1m).
参考数据:sin48°=0.7,cos48°=0.7,tan48°=1.1,cos65°=0.4,tan65°=2.1
查看答案和解析>>
科目:初中数学 来源: 题型:
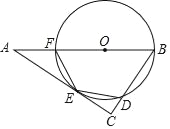
【题目】如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.
(1)求证:∠C=90°;
(2)当BC=3,sinA=![]() 时,求AF的长.
时,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com