

| A.①② | B.①③④ | C.①②④ | D.①②③④ |
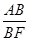 =
=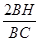 ,无法直接用相似来求出,那么可通过相等的比例关系式来进行转换,不难发现三角形BEC中,∠ABC=60°,那么BC和BE存在倍数关系,即BC=2BE,因此如果证得
,无法直接用相似来求出,那么可通过相等的比例关系式来进行转换,不难发现三角形BEC中,∠ABC=60°,那么BC和BE存在倍数关系,即BC=2BE,因此如果证得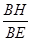 =
=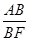 ,可发现这个比例关系式正好是相似三角形BEH和BAF的两组对应线段,因此本题的结论也是正确的.
,可发现这个比例关系式正好是相似三角形BEH和BAF的两组对应线段,因此本题的结论也是正确的.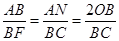 ,将这个结论和②的结论进行置换即可得出:BD=BO=BH=BG,因此可证MB和圆的半径相等即可得出BM=BD的结论.如果连接NC,在三角形ANC中∠ANC=∠ABC=60°,因此AN=2NC,NC就是半径的长.通过相似三角形BME和CAE可得出
,将这个结论和②的结论进行置换即可得出:BD=BO=BH=BG,因此可证MB和圆的半径相等即可得出BM=BD的结论.如果连接NC,在三角形ANC中∠ANC=∠ABC=60°,因此AN=2NC,NC就是半径的长.通过相似三角形BME和CAE可得出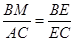 ,而在直角三角形BEC中,BE:EC=tan30°,而在直角三角形ANC中,NC:AC=tan30°,因此
,而在直角三角形BEC中,BE:EC=tan30°,而在直角三角形ANC中,NC:AC=tan30°,因此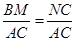 ,即可得出BM=NC=BO=BD.因此该结论也成立.
,即可得出BM=NC=BO=BD.因此该结论也成立.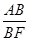 =
=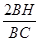 ,∠ABC=60°,那么BC=2BE,因此
,∠ABC=60°,那么BC=2BE,因此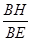 =
=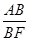 ,所以本题的结论也是正确的.
,所以本题的结论也是正确的.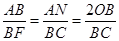 ,BD=BO=BH=BG,BM=BD.
,BD=BO=BH=BG,BM=BD.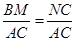 ,∴BM=NC=BO=BD.
,∴BM=NC=BO=BD.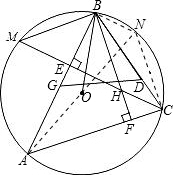


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 BC;
BC;
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com