
����Ŀ����ͼ��������y��ax2+bx+c��a��0���ĶԳ���Ϊֱ��x��1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ���4ac��b2������3a+c��0���۵�x��0ʱ��y��x���������С���ܵ�y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3���ݷ���ax2+bx+c��0����������x1����1��x2��3�����н�����ȷ�ĸ����ǣ�������
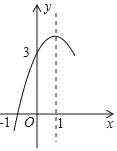
A. 4�� B. 3�� C. 2�� D. 1��
���𰸡�B
��������
������������x��Ľ�������ɶ��������жϣ��ɶԳ��᷽�̵õ�b����2a��Ȼ�����x����1ʱ����ֵΪ0�ɵõ�3a+c��0����ɶ��������жϣ����ݶ��κ��������ʶ��������ж������������ߵĶԳ��Եõ���������x���һ����������Ϊ��3��0������ɶ��������жϣ�������������x���Ϸ�����Ӧ���Ա����ķ�Χ�ɶ��������жϣ�
�⣺����������x����2�����㣬
��b2��4ac��0����4ac��b2����������ȷ��
��x����![]() ��1����b����2a��
��1����b����2a��
��x����1ʱ��y��0����a��b+c��0��
��a+2a+c��0����3a+c��0������������
�������ߵĶԳ���Ϊֱ��x��1���������£�
����x��1ʱ��y��x�������С��������������
�������ߵĶԳ���Ϊֱ��x��1��
���㣨��1��0������ֱ��x��1�ĶԳƵ������Ϊ��3��0����
������ax2+bx+c��0����������x1����1��x2��3����������ȷ��
����������x���������������1��0������3��0����
������1��x��3ʱ��y��0����������ȷ.
��ѡ��B��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
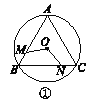
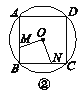
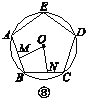
����Ŀ����ͼ�٢ڢۢ���M��N�ֱ��ǡ�O���ڽ���������ABC��������ABCD���������ABCDE��������n����ABCDEFG���ı�AB��BC�ϵĵ�����BM��CN������OM��ON.
(1)��ͼ���С�MON�Ķ�����
(2)ͼ��������MON�Ķ�����________��ͼ���С�MON�Ķ�����________��
(3)��̽����MON�Ķ�������n���εı���n�Ĺ�ϵ(ֱ��д����)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�AG��BC�ڵ�G��AF��DE�ڵ�F����EAF=��GAC��
��1����֤����ADE�ס�ABC��
��2����AD=3��AB=5����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
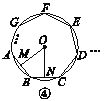
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij���������ţ��ŵĸ߶���5�ף�CB��DB������AC����б��Ϊ45����Ϊ�������˹��ţ��������ž��������¶ȣ�ʹ������DC���¶�Ϊi= ![]() ��3�������½���������2�������е�������ԭ�½ǣ�A�㴦��6��һ�����Ƿ���Ҫ���ԣ����ο����ݣ�
��3�������½���������2�������е�������ԭ�½ǣ�A�㴦��6��һ�����Ƿ���Ҫ���ԣ����ο����ݣ� ![]() ��1.414��
��1.414�� ![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
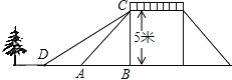
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90����ADƽ�֡�BAC����A��C��D�����Բ��б��AB���ڵ�E������DE��
��1����֤��AC=AE��
��2����AC=6��CB=8������ACD���Բ��ֱ����
�鿴�𰸺ͽ���>>
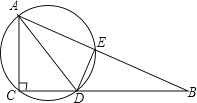
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BCD�ڽ��ڡ�O��ֱ��AB������CD���е�M��AE��BC���ӳ����ڵ�E������AC����EAC����ABD��30�㣮
��1����֤����BCD�ǵȱ������Σ�
��2����֤��AE�ǡ�O�����ߣ�
��3����CE��2�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ѧУ��ʵ��¥������һ����ѧ¥��С����ʵ��¥�Ĵ���C��ý�ѧ¥����D������Ϊ18�㣬��ѧ¥�ײ�B�ĸ���Ϊ20�㣬����ʵ��¥���ѧ¥֮��ľ���AB=30m��
��1������BCD�Ķ�����
��2�����ѧ¥�ĸ�BD���������ȷ��0.1m���ο����ݣ�tan20����0.36��tan18����0.32��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��x2��4x��3.
(1)���䷽������ͼ��Ķ���C�����꣬�������ú����ĺ���ֵ���Ա������������仯�������
(2)����ͼ����x��Ľ���A��B�����꣬����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABCD��һ����AD=8��������ABCD�۵���ʹ�ö���B����CD���ϵ�P�㴦����֪�ۺ����BC���ڵ�O������AP��OP��OA��

��1����֤����OCP�ס�PDA��
��2������OCP����PDA�������Ϊ1��4�����AB�ij���
��3����ͼ2����ȥ�ۺ�AO���߶�OP������BP������M���߶�AP�ϣ���M���P��A���غϣ�������N���߶�AB���ӳ����ϣ���BN=PM������MN��PB�ڵ�F����ME��BP�ڵ�E��̽��������M��N���ƶ������У��߶�EF���߶�PB�к�������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com