
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示第m排,从左到右第n个数,如(3,2)表示正整数5,(4,3)表示正整数9,则(100,16)表示的正整数是4966.
将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示第m排,从左到右第n个数,如(3,2)表示正整数5,(4,3)表示正整数9,则(100,16)表示的正整数是4966.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
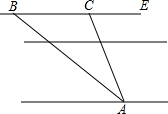 在一次测量活动中,同学们想测量某高速公路的宽度.如图,他们在该高速公路的东侧选定一广告牌A,并在西侧防护带的外沿B处观察,此时视线BA与外沿BE所成的夹角是30°,沿外沿BE向北走了8米到C处,再观察A,此时视线CA与外沿所成的夹角∠ACE=60°,已纪该高速公路西侧防护带宽1米.求此高速公路的宽约为多少米.(结果精确到1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次测量活动中,同学们想测量某高速公路的宽度.如图,他们在该高速公路的东侧选定一广告牌A,并在西侧防护带的外沿B处观察,此时视线BA与外沿BE所成的夹角是30°,沿外沿BE向北走了8米到C处,再观察A,此时视线CA与外沿所成的夹角∠ACE=60°,已纪该高速公路西侧防护带宽1米.求此高速公路的宽约为多少米.(结果精确到1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
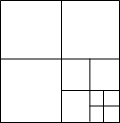 连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…,重复这样的操作,则5次操作后右下角的小正方形面积是$(\frac{1}{4})^{5}$.
连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…,重复这样的操作,则5次操作后右下角的小正方形面积是$(\frac{1}{4})^{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
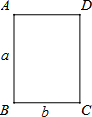 如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )| A. | V甲>V乙 S甲=S乙 | B. | V甲<V乙 S甲=S乙 | ||
| C. | V甲=V乙 S甲=S乙 | D. | V甲>V乙 S甲<S乙 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.
如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com