
【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:
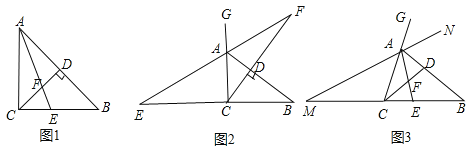
(习题回顾)已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
(变式思考)如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
(探究廷伸)如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
【答案】【习题回顾】证明见解析;【变式思考】∠CEF=∠CFE,理由见解析;【探究思考】∠M+∠CFE=90°,理由见解析.
【解析】
根据三角形的外角的性质证明;
【变式思考】
根据角平分线的定义、直角三角形的性质解答;
【探究廷伸】
同(1)、(2)的方法相同.
∵∠ACB=90°,CD是高,∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,∴∠B=∠ACD.
∵AE是角平分线,∴∠CAF=∠DAF.
∵∠CFE=∠CAF+∠ACD∠CEF=∠DAF+∠B,∴∠CEF=∠CFE;
变式思考:∠CEF=∠CFE.证明如下:
∵AF为∠BAG的角平分线,∴∠GAF=∠DAF.
∵CD为AB边上的高,∴∠ACB=90°,∴∠ADF=∠ACE=90°.
又∵∠CAE=∠GAF,∴∠CEF=∠CFE;
探究思考:∠M+∠CFE=90°.证明如下:
∵C、A、G三点共线 AE、AN为角平分线,∴∠EAN=90°.
又∵∠GAN=∠CAM,∴∠MAE=90°,∴∠M+∠CEF=90°.
∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,∴∠CEF=∠CFE,∴∠M+∠CFE=90°.


科目:初中数学 来源: 题型:
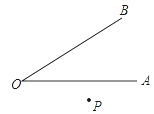
【题目】如图,已知∠AOB=a外有一点P,画点P关于直线OA的对称点P′,再作点P′关于直线OB的对称点P″.
(1)试猜想∠POP″与a的大小关系,并说出你的理由.
(2)当P为∠AOB 内一点或∠AOB边上一点时,上述结论是否成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是平方单位(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( )
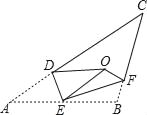
A. 40° B. 41° C. 42° D. 43°
查看答案和解析>>
科目:初中数学 来源: 题型:
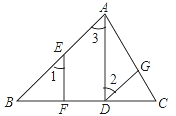
【题目】如图,已知△ABC中,AD⊥BC于点D,E为AB边上任意一点,EF⊥BC于点F,∠1=∠2.求证:DG∥AB.请把证明的过程填写完整.
证明:∵AD⊥BC,EF⊥BC( ),
∴∠EFB=∠ADB=90°(垂直的定义)
∴EF∥ ( )
∴∠1= ( )
又∵∠1=∠2(已知)
∴ ( )
∴DG∥AB( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是( )

A.90° B.120° C.135° D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是某省2010年教育发展情况有关数据:
全省共有各级各类学校25000所,其中小学12500所,初中2000所,高中450所,其它学校10050所;全省共有在校学生995万人,其中小学440万人,初中200万人,高中75万人,其它280万人;全省共有在职教师48万人,其中小学20万人,初中12万人,高中5万人,其它11万人.
请将上述资料中的数据按下列步骤进行统计分析.
(1)整理数据:请设计一个统计表,将以上数据填入表格中.
(2)描述数据:下图是描述全省各级各类学校所数的扇形统计图,请将它补充完整.
(3)分析数据:
①分析统计表中的相关数据,小学、初中、高中三个学段的师生比,最小的是哪个学段?请直接写出.(师生比=在职教师数︰在校学生数)
②根据统计表中的相关数据,你还能从其它角度分析得出什么结论吗?(写出一个即可)
③从扇形统计图中,你得出什么结论?(写出一个即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.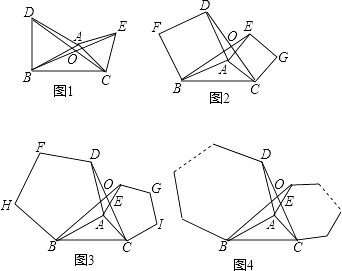
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC=(填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为(用含n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com