【题目】如图，正五边形的边长为2，连对角线AD，BE，CE，线段AD分别与BE和CE相交于点M，N，则MN= ．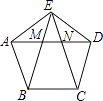 
【答案】3﹣ 
【解析】解：∵∠BAE=∠AED=108°，
∵AB=AE=DE，
∴∠ABE=∠AEB=∠EAD=36°，
∴∠AME=180°﹣∠EAM﹣∠AEM=108°，
∵∠AEN=108°﹣36°=72°，∠ANE=36°+36°=72°，
∴∠AEN=∠ANE，
∴AE=AN，
同理DE=DM，
∴AE=DM，
∵∠EAD=∠AEM=∠ADE=36°，
∴△AEM∽△ADE，
∴ 
，
∴AE2=AMAD
∴AN2=AMAD；
∴22=（2﹣MN）（4﹣MN），
∴MN=3﹣ ；
所以答案是：3﹣ ．
【考点精析】解答此题的关键在于理解正多边形和圆的相关知识，掌握圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】阅读理解：
小聪在解方程组
时，发现方程组中①和②之间存在一定的关系，他发现了一种“整体代换”法，具体解法如下：
解：将方程②变形为：
即
把方程①代入方程③得：
解得
把代入方程①得
∴方程组的解是
（1）模仿小聪的解法，解方程组
（2）已知x，y满足方程组
，解答：
（ⅰ）求
的值；
（ⅱ）求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°．求：
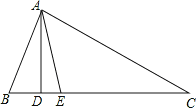
（1）∠BAE的度数；
（2）∠DAE的度数；
（3）探究：小明认为如果条件∠B=70°，∠C=30°改成∠B-∠C=40°，也能得出∠DAE的度数？若能，请你写出求解过程；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知l1∥l2，MN分别和直线l1、l2交于点A、B，ME分别和直线l1、l2交于点C、D，点P在MN上（P点与A、B、M三点不重合）．
（1）如果点P在A、B两点之间运动时，∠α、∠β、∠γ之间有何数量关系请说明理由；
（2）如果点P在A、B两点外侧运动时，∠α、∠β、∠γ有何数量关系（只须写出结论）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠MON＝90°，点A，B分别在射线OM，ON上运动，BE平分∠ABN，BE的反向延长线与∠BAO的平分线交于点C.
(1)当点A，B移动后，∠BAO＝45°时，∠C＝________；
(2)当点A，B移动后，∠BAO＝60°时，∠C＝________；
(3)由(1)(2)猜想∠C是否随点A，B的移动而发生变化，并说明理由．
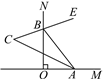
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】经过建设者三年的努力，贯穿四川的“遂内高速”正式通车，已知原来从遂宁到内江的公路长150km，高速公路路程比公路缩短30km，一辆小车从遂宁到内江走高速公路的平均速度可以提高到原来的1.5倍，用时比原来减少1小时，求小车原来的平均速度和走高速的平均速度．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
