
 已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α≤180)得到矩形A1BC1D1,此时A1B,C1D1这两边所在的直线分别与CD边所在的直线相交于点P、Q,当DP:DQ=1:2时,DP的长为5或1+$\sqrt{11}$.
已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α≤180)得到矩形A1BC1D1,此时A1B,C1D1这两边所在的直线分别与CD边所在的直线相交于点P、Q,当DP:DQ=1:2时,DP的长为5或1+$\sqrt{11}$. 分析 如图,作辅助线;首先证明四边形PMBC、四边形PBC′N均是矩形;其次证明△BPM≌△QPN,得到PB=PQ,此为解决问题的关键性结论;证明DP=PQ=PB;设DP=λ,运用勾股定理列出关于λ的方程,求出λ即可解决问题.
解答  解:情况一:如图,过点P作PM⊥AB,PN⊥C′D′;
解:情况一:如图,过点P作PM⊥AB,PN⊥C′D′;
则四边形PMBC、四边形PBC′N均是矩形,
∴∠PNQ=∠PMB=∠CPM=∠C′NP=90°;
PM=BC=BC′=PN;
∴∠BPM=90°-∠BPC=∠QPN;
在△BPM与△QPN中,
$\left\{\begin{array}{l}{∠MPB=∠NPQ}\\{PM=PN}\\{∠PMB=∠PNQ}\end{array}\right.$,
∴△BPM≌△QPN,
∴PB=PQ;而DP:DQ=1:2,
∴DP=PQ=PB;设DP=λ,
则PB=λ,CP=8-λ;在Rt△BCP中,
PB2=PC2+BC2,
即λ2=(8-λ)2+42,
解得:λ=5,即DP=5,
情况二:如图
同理求得DP=1+$\sqrt{11}$,DP=1-$\sqrt{11}$(舍去)
故答案为5或1+$\sqrt{11}$.
点评 该题主要考查了矩形的性质、勾股定理、旋转变换的性质等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用矩形的性质、旋转变换的性质等几何知识点来分析、判断、推理或解答.


科目:初中数学 来源: 题型:选择题
| A. | 2sinαcosα | B. | sinα | C. | cosα | D. | cos2α |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
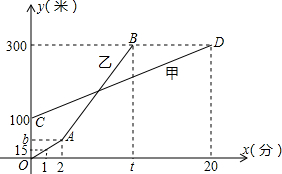 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
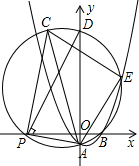 如图,在平面直角坐标系中,抛物线y═$\frac{1}{2}$x2+bx+c经过点A(0,-1),B(2,0)P(t,0)是x轴负半轴上一动点,过点P作PA的垂线交△PAB的外接圆于点C,△PAB的外接圆与y轴交于点D,与抛物线在第一象限限交于点E.
如图,在平面直角坐标系中,抛物线y═$\frac{1}{2}$x2+bx+c经过点A(0,-1),B(2,0)P(t,0)是x轴负半轴上一动点,过点P作PA的垂线交△PAB的外接圆于点C,△PAB的外接圆与y轴交于点D,与抛物线在第一象限限交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.
如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 工种 | A | B |
| 月收入(元/人) | 3600 | 1800 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,⊙P的半径是1,圆心P在函数y=$\frac{3}{x+2}$(x>-2)的图象上运动,当⊙P与坐标轴相切时,圆心P的坐标为(1,1)或(-1,3).
如图,⊙P的半径是1,圆心P在函数y=$\frac{3}{x+2}$(x>-2)的图象上运动,当⊙P与坐标轴相切时,圆心P的坐标为(1,1)或(-1,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com