
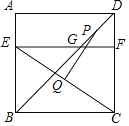
【题目】如图,正方形ABCD的边长为12,点E在边AB上,BE=8,过点E作EF∥BC,分别交BD、CD于G、F两点.若点P、Q分别为DG、CE的中点,则PQ的长为_____.
科目:初中数学 来源: 题型:
【题目】如图,一个长方形盒子的长、宽、高分别是4cm,4cm,6cm
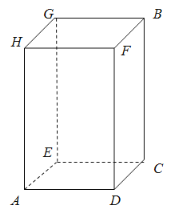
(1)一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,请你帮蚂蚁设计一条最短的路线,蚂蚁要爬行的最短路线是多少?
(2)若将一根木棒放进盒子里并能盖上盖子,则能放入改盒子里的木棒的最大长是多少cm?(结果可保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并回答问题:
如果两个两位数的十位数字相同,个位数字相加为10,那么能立即说出这两个两位数的乘积,如果这两个两位数分别写作![]() 和
和![]() (即十位数字为
(即十位数字为![]() ,个位数字分别为
,个位数字分别为![]() 、
、![]() ,
,![]() ,
,![]() ),那么它们的乘积是一个4位数,前两位数字是
),那么它们的乘积是一个4位数,前两位数字是![]() 和
和![]() 的乘积,后两位数字就是
的乘积,后两位数字就是![]() 和
和![]() 的乘积,如:
的乘积,如:![]() ,
,![]() .
.
(1)![]() ________;
________;
(2)设这两个两位数的十位数字为![]() ,个位数字分别为
,个位数字分别为![]() 和
和![]() ,
,![]() ,通过计算验证这两个两位数的乘积为
,通过计算验证这两个两位数的乘积为![]()
![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
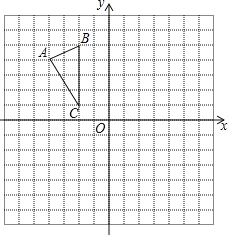
【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣4,4),B(﹣2,5),C(﹣2,1).
(1)平移△ABC,使点C移到点C1(﹣2,﹣4),画出平移后的△A1B1C1,并写出点A1,B1的坐标;
(2)将△ABC绕点(0,3)旋转180°,得到△A2B2C2,画出旋转后的△A2B2C2;
(3)求(2)中的点C旋转到点C2时,点C经过的路径长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,OB、OM、ON,是
,OB、OM、ON,是![]() 内的射线.
内的射线.
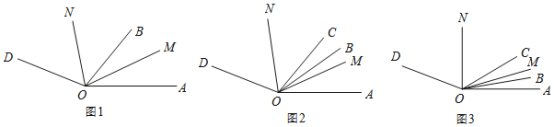
(1)如图 1,若 OM 平分 ![]() , ON平分
, ON平分![]() .当射线OB 绕点O 在
.当射线OB 绕点O 在![]() 内旋转时,
内旋转时,![]() = 度.
= 度.
(2)OC也是![]() 内的射线,如图2,若
内的射线,如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ,当射线OB绕点O在
,当射线OB绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小.
的大小.
(3)在(2)的条件下,当射线OB从边OA开始绕O点以每秒![]() 的速度逆时针旋转t秒,如图3,若
的速度逆时针旋转t秒,如图3,若![]() ,求t的值.
,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个四位自然数的百位数字大于或等于十位数字,且千位数字等于百位数字与十位数字的和,个位数字等于百位与十位数字的差,则我们称这个四位数为亲密数,例如:自然数4312,其中3>1,4=3+1,2=3-1,所以4312是亲密数;
(1)最小的亲密数是 ,最大的亲密数是 ;
(2)若把一个亲密数的千位数字与个位数字交换,得到的新数叫做这个亲密数的友谊数,请证明任意一个亲密数和它的友谊数的差都能被原亲密数的十位数字整除;
(3)若一个亲密数的后三位数字所表示的数与千位数字所表示的数的7倍之差能被13整除,请求出这个亲密数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com