
【题目】如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.

下列判断:
①当x>0时,y1>y2;
②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在;
④使得M=1的x值是![]() 或
或![]() .其中正确的个数是( )
.其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
科目:初中数学 来源: 题型:
【题目】我们在学习《从面积到乘法公式》时,曾用两种不同的方法计算同一个图形的面积,探索了单项式乘多项式的运算法则:m(a+b+c)=ma+mb+mc(如图1),多项式乘多项式的运算法则:
(a+b)(c+d)=ac+ad+bc+bd(如图2),以及完全平方公式:(a+b)2=a2+2ab+b2(如图3).
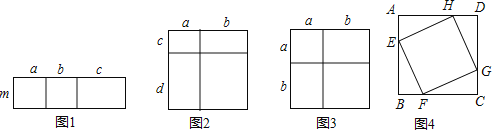
把几个图形拼成一个新的图形,通过图形面积的计算,常常可以得到一些等式,这是研究数学问题的一种常用方法.
(1)请设计两个图形说明一下两个等式成立(画出示意图,并标上字母)
①(a+b)(2a+b)=2a2+3ab+b2
②(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
(2)如图4,它是由四个形状、大小完全相同的直角三角形与中间的小正方形EFGH拼成的一个大正方形ABCD.如果每个直角三角形的较短的边长为a,较长的边长为b,最长的边长为c.试用两种不同的方法计算这个大正方形的面积,你能发现直角三角形的三边长a、b、c的什么数量关系?(注:写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天) | 豪华间(元/人/天) | 贵宾间(元/人/天) | |
三人间 | 50 | 100 | 500 |
双人间 | 70 | 150 | 800 |
单人间 | 100 | 200 | 1500 |
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A(3,0),B两点,与y轴交于点C,点M(
与x轴交于A(3,0),B两点,与y轴交于点C,点M(![]() ,5)是抛物线
,5)是抛物线![]() 上一点,抛物线
上一点,抛物线![]() 与抛物线
与抛物线![]() 关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′
关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′
(1)求抛物线C1的解析式;
(2)过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D. P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
(1)如图①,边长为4的等边△OAB位于平面直角坐标系中,将△OAB折叠,使点B落在OA的中点处,则折痕长为 ;
(2)如图②,矩形OABC位于平面直角坐标系中,其中OA=8,AB=6,将矩形沿线段MN折叠,点B落在x轴上,其中AN=![]() AB,求折痕MN的长;
AB,求折痕MN的长;
问题解决:
(3)如图③,四边形OABC位于平面直角坐标系中,其中OA=AB=6,CB=4,BC∥OA,AB⊥OA于点A,点Q(4,3)为四边形内部一点,将四边形折叠,使点B落在x轴上,问是否存在过点Q的折痕,若存在,求出折痕长,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P的横坐标和纵坐标相等,则称点P为等值点.例如点
(1,1),(-2,-2),(![]() ,
,![]() ),…,都是等值点.已知二次函数
),…,都是等值点.已知二次函数![]() 的
的
图象上有且只有一个等值点![]() ,且当m≤x≤3时,函数
,且当m≤x≤3时,函数 ![]() 的最小值为-9,最大值为-1,则m的取值范围是__________.
的最小值为-9,最大值为-1,则m的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
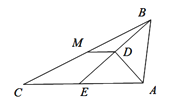
【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com