
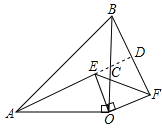
【题目】如图,已知,等腰Rt△OAB中,∠AOB=90°,等腰Rt△EOF中,∠EOF=90°,连结AE、BF.

求证:(1)AE=BF;(2)AE⊥BF.
【答案】见解析
【解析】
(1)可以把要证明相等的线段AE,CF放到△AEO,△BFO中考虑全等的条件,由两个等腰直角三角形得AO=BO,OE=OF,再找夹角相等,这两个夹角都是直角减去∠BOE的结果,所以相等,由此可以证明△AEO≌△BFO;
(2)由(1)知:∠OAC=∠OBF,∴∠BDA=∠AOB=90°,由此可以证明AE⊥BF
解:(1)证明:在△AEO与△BFO中,
∵Rt△OAB与Rt△EOF等腰直角三角形,
∴AO=OB,OE=OF,∠AOE=90°-∠BOE=∠BOF,
∴△AEO≌△BFO,
∴AE=BF;
( 2)延长AE交BF于D,交OB于C,则∠BCD=∠ACO
由(1)知:∠OAC=∠OBF,
∴∠BDA=∠AOB=90°,
∴AE⊥BF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,BD分别与AE、AF相交于G、H.

(1)在图中找出与△ABE相似的三角形,并说明理由;
(2)若AG=AH,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交ABCD的四条边于E、G、F、H四点,连接EG、GF、FH、HE.

(1)如图①,四边形EGFH的形状是___;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是___;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是___;
(4)如图④,在(3)的条件下,若AC⊥BD,四边形EGFH的形状是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形OABCDE中,点E(﹣2,0),将该正六边形向右平移a(a>0)个单位后,恰有两个顶点落在反比例函数y=![]() (k>0)的图象上,则k的值为__.
(k>0)的图象上,则k的值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E是△ABC内一点,若∠AEB=∠CED=90°,AE=BE,CE=DE=2,则图中阴影部分的面积等于__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,活动课上,小玥想要利用所学的数学知识测量某个建筑地所在山坡AE的高度,她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1:1的斜坡按速度20米/分步行15分钟到达C处,此时,测得点A的俯角是15°.图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出建筑地所在山坡AE的高度AB.(精确到0.1米,参考数据:![]() ≈1.41).
≈1.41).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com