
分析 (1)根据特殊角的函数值即可求出答案.
(2)先化简原方程组,然后根据二元一次方程组的解法即可
解答 解:(1)原式=1-$\frac{1}{2}$+3+4
=8-$\frac{1}{2}$
=$\frac{15}{2}$
(2)原方程组化为$\left\{\begin{array}{l}{5x+5y=-1①}\\{x+5y=3②}\end{array}\right.$
①-②得:4x=-4
x=-1
将x=-1代入①中,y=$\frac{4}{5}$
解得:$\left\{\begin{array}{l}{x=-1}\\{y=\frac{4}{5}}\end{array}\right.$
点评 本题考查学生的计算能力,解题的关键熟练运用运算法则,本题属于基础题型.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
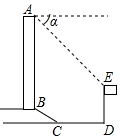 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,求大楼AB的高度是多少?(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,求大楼AB的高度是多少?(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
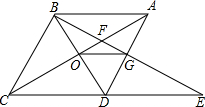 如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是①④.(把所有正确结论的序号都填在横线上)
如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是①④.(把所有正确结论的序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形OABC的边OA,OC分别在坐标轴上,OA=4,OC=8,把△ABC沿着AC折叠.点B落在点B′处,AB′交y轴于点D,则点D的坐标是(0,3).
如图,矩形OABC的边OA,OC分别在坐标轴上,OA=4,OC=8,把△ABC沿着AC折叠.点B落在点B′处,AB′交y轴于点D,则点D的坐标是(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com