练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．-32-|-53|×（-$\frac{2}{5}$）3-18÷（-3）2．

    分析 原式先计算乘方及绝对值运算，再计算乘除运算，最后算加减运算即可得到结果．

    解答 解：原式=-9+8-2=-3．

    点评 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

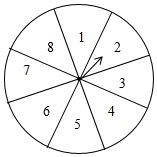    5．如图，一个均匀的转盘被平均分成8等份，分别标有“1，2，3，4，5，6，7，8”这8个数字，转动转盘，当转盘停止后，指针指向的数字即为转出的数字．游戏规则如下：甲、乙两个人参与游戏，甲转动转盘，乙猜数，若猜的数与转盘转出的数相符，则乙获胜；若结果不相符，则甲获胜．（若指针恰好指在分割线上，那么重转一次）．
    （1）如果乙猜是“数9”，则乙获胜的概率为0；
    （2）如果乙猜是“3的倍数”，则甲获胜的概率是$\frac{3}{4}$；
    （3）如果乙猜是“偶数”，这个游戏对双方公平吗？请说明；
    （4）如果你是乙，请设计一种猜数方法，使自己获胜的可能性较大．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图1，在梯形ABCD中，∠A=90°，AD∥BC，AD=2，AB=3，BC=8，点F是线段DC的中点，点G是线段DF上的一个动点（不与点F重合），连接BG并延长线段AD延长线于点P．
    （1）若AB+DP=BP，求PD的长．
    （2）如图2，点E是BP的中点．
    ①若设DP=x，EF=y，求y与x的函数关系式并写出定义域．
    ②连接DE和PF，若DE=PF，求PD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

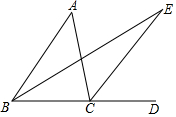    3．如图，CD是△ABC的边BC的延长线，射线BE、CE相交于点E．
    （1）若BE、CE分别平分∠ABC、∠ACD，求证：∠E=$\frac{1}{2}∠A$；（提示：∠E=∠ECD-∠EBC）
    （2）根据（1）的结论及提示猜想：若∠EBC=$\frac{1}{n}∠ABC$，∠ECD=$\frac{1}{n}∠ACD$，∠A=60°，则∠E的度数为$\frac{60°}{n}$（用含n的式子表示）
    （3）在（2）的条件下，当CE∥AB，∠ABC=30°时，求n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

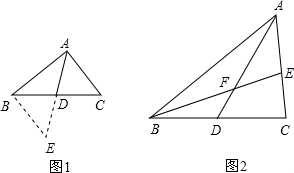    10．某校数学课外兴趣小组活动时，老师提出如下问题：
    【探究】如图1，△ABC中，若AB=8，AC=6，点D是BC的中点，试探究BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE=AD，请补充完整证明“△ADC≌△EDB”的推理过程．
    （1）求证：△ADC≌△EDB
    证明：∵延长AD到点E，使DE=AD
    在△ADC和△EDB中AD=ED（已作）∠ADC=∠EDB（对顶角相等）     CD=BD（中点定义）
    ∴△ADC≌△EDB（SAS）
    （2）探究得出AD的取值范围是1＜AD＜7；
    【感悟】解题时，条件中若出现“中点”“中线”等字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．
    【问题解决】
    （3）如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AC=BF．
    求证：∠BFD=∠CAD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．因式分解：ax2-a的结果是a（x+1）（x-1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．4和12的最小公倍数是12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．据统计，2014年天猫双十一购物节24小时内销售额达到571亿元，共产生了约2.8亿个包裹．则近似数“571亿”用科学记数法可表示为5.71×1010，而“2.8亿”精确到千万位．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．已知一个正方体的体积是729立方厘米，现在要在它的8个角上分别截去8个大小相同的小正方形，使得截去后余下的体积是665立方厘米，则截去的每个小正方体的棱长是（　　）
    A．8厘米B．6厘米C．4厘米D．2厘米

    查看答案和解析>>

    同步练习册答案