
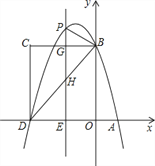
【题目】如图,在平面直角坐标系中,抛物线y=-![]() x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(-3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(-3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
【答案】(1)解析式为![]() ;
;
(2)PG=-![]() m2-
m2-![]() m;
m;
(3)m的值为-1或![]()
【解析】试题分析:(1)将A(1,0),B(0,4)代入y=-![]() x2+bx+c,运用待定系数法即可求出抛物线的解析式;
x2+bx+c,运用待定系数法即可求出抛物线的解析式;
(2)由E(m,0),B(0,4),得出P(m,-![]() m2-
m2-![]() m+4),G(m,4),则PG=-
m+4),G(m,4),则PG=-![]() m2-
m2-![]() m+4-4=-
m+4-4=-![]() m2-
m2-![]() m,点P在直线BC上方时,故需要求出m的取值范围;
m,点P在直线BC上方时,故需要求出m的取值范围;
(3)先由抛物线的解析式求出D(-3,0),则当点P在直线BC上方时,-2<m<0.再运用待定系数法求出直线BD的解析式为y=![]() x+4,于是得出H(m,
x+4,于是得出H(m, ![]() m+4).当以P、B、G为顶点的三角形与△DEH相似时,由于∠PGB=∠DEH=90°,所以分两种情况进行讨论:①△BGP∽△DEH;②△PGB∽△DEH.都可以根据相似三角形对应边成比例列出比例关系式,进而求出m的值.
m+4).当以P、B、G为顶点的三角形与△DEH相似时,由于∠PGB=∠DEH=90°,所以分两种情况进行讨论:①△BGP∽△DEH;②△PGB∽△DEH.都可以根据相似三角形对应边成比例列出比例关系式,进而求出m的值.
试题解析:
(1)解析式为![]()
(2)∵E(m,0),B(0,4),PE⊥x轴交抛物线于点P,交BC于点G,
∴P(m,- ![]() m2-
m2-![]() m+4),G(m,4),
m+4),G(m,4),
∴PG=-![]() m2-
m2-![]() m+4-4=-
m+4-4=-![]() m2-
m2-![]() m;
m;
(3)在(2)的条件下,存在点P,使得以P、B、G为顶点的三角形与△DEH相似.
当点P在直线BC上方时,-3<m<0.
设直线BD的解析式为y=kx+4,
将D(-3,0)代入,得-3k+4=0,解得k=![]() .
.
∴直线BD的解析式为y=![]() x+4.∴H(m,
x+4.∴H(m, ![]() m+4).
m+4).
分两种情况:
①如果△BGP∽△DEH,那么![]() ,即
,即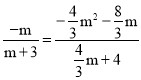
由-3<m<0,解得m=-1.
②如果△PGB∽△DEH,那么![]() ,即
,即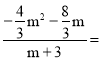
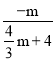 ,
,
由-3<m<0,解得m=![]() .
.
综上所述,在(2)的条件下,存在点P,使得以P、B、G为顶点的三角形与△DEH相似,此时m的值为-1或![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A= ![]() ∠B=
∠B= ![]() ∠C
∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整. 因为EF∥AD,
所以∠2=(),
又因为∠1=∠2,
所以∠1=∠3(),
所以AB∥(),
所以∠BAC+=180°(),
因为∠BAC=80°,
所以∠AGD= . 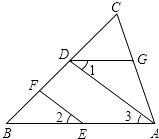
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=kx+b,其中常数k>0,b<0,那么这个函数的图象不经过的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com