
分析 根据方程有实数根结合根的判别式即可得出关于k的一元一次不等式,解之即可得出k的取值范围,设方程2x2+4x+3k=0的两个根为x1、x2,根据根与系数的关系结合${{x}_{1}}^{2}+{{x}_{2}}^{2}$=7即可得出关于k的一元一次方程,解之即可得出k的值,结合k的取值范围即可得出结论.
解答 解:∵方程2x2+4x+3k=0有实数根,
∴△=42-4×2×3k=16-24k≥0,
解得:k≤$\frac{2}{3}$.
设方程2x2+4x+3k=0的两个根为x1、x2,
则有:x1+x2=-2,x1•x2=$\frac{3}{2}$k,
∵${{x}_{1}}^{2}+{{x}_{2}}^{2}$=7,
∴$({x}_{1}+{x}_{2})^{2}$-2x1•x2=4-3k=7,
解得:k=-1.
故k的值为-1.
点评 本题考查了根与系数的关系以及根的判别式,熟练掌握“x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$”是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
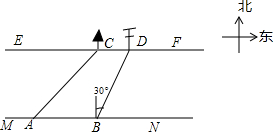 在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(结果保留根号)
在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com