分析:本题大致的思路是连接BC、BD,分别在Rt△CAB和Rt△BAD中,求出∠CAD和∠CAB的度数,然后根据D点的不同位置分类讨论.
解答: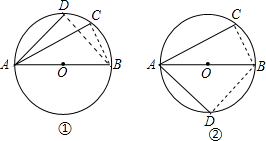
解:本题分两种情况:(如图)
①当AD在AB上方时,连接BD、BC,
则∠ADB=∠ACB=90°,
Rt△ADB中,AD=
,AB=2,
∴∠DAB=45°,
Rt△ACB中,AC=
,AB=2,
∴∠CAB=30°,
∴∠CAD=∠DAB-∠CAB=15°,
②当AD在AB下方时,同①可求得∠CAD=75°,
故答案为:15°或75°.
点评:本题考查的是圆周角定理及直角三角形的性质,比较简单,但在解答时要注意分两种情况讨论,不要漏解,难度适中.
