
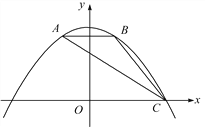
����Ŀ����ͼ��������y��ax2��bx��c������ABC���������㣬��y���ཻ��(0�� ![]() )����A����Ϊ(��1��2)����B�ǵ�A����y��ĶԳƵ㣬��C��x����������ϣ�
)����A����Ϊ(��1��2)����B�ǵ�A����y��ĶԳƵ㣬��C��x����������ϣ�
��1����������ߵĺ�������ʽ��
��2����FΪ�߶�AC��һ���㣬����F��FE��x�ᣬFG��y�ᣬ����ֱ�Ϊ��E��G�����ı���OEFGΪ������ʱ�������F�����ꣻ
��3������2���е�������OEFG��OC����ƽ�ƣ���ƽ���е�������OEFGΪ������DEFG������E�͵�C�غ�ʱֹͣ�˶�����ƽ�Ƶľ���Ϊt�������εı�EF��AC���ڵ�M��DG���ڵ�ֱ����AC���ڵ�N������DM���Ƿ����������t��ʹ��DMN�ǵ��������Σ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��y=��![]() x2+
x2+![]() ����2����1��1������3������DMN�ǵ���������ʱ��t��ֵΪ
����2����1��1������3������DMN�ǵ���������ʱ��t��ֵΪ![]() ��3��
��3��![]() ��1��
��1��
�������������������1���������ߵĶ���Ϊ��0��![]() ����Ȼ��ֻ�����ô���ϵ�������Ϳ���������ߵĺ�����ϵ����ʽ��
����Ȼ��ֻ�����ô���ϵ�������Ϳ���������ߵĺ�����ϵ����ʽ��
��2��������F�ڵ�һ����ʱ����ͼ1���������C�����ֱ꣬��AC�Ľ���ʽ����������OEFG�ı߳�Ϊp����F��p��p��������ֱ��AC�Ľ���ʽ���Ϳ������F�����ꣻ������F�ڵڶ�����ʱ��ͬ���������F�����꣬��ʱ��F�����߶�AC�ϣ�����ȥ��
��3������M��MH��DN��H����ͼ2������ɵ�0��t��2��Ȼ��ֻ����t��ʽ�ӱ�ʾDN��DM2��MN2���������������DN=DM����ND=NM����MN=MD�����۾Ϳɽ�����⣮
�����������1������B�ǵ�A����y��ĶԳƵ㣬
�������ߵĶԳ���Ϊy�ᣬ
�������ߵĶ���Ϊ��0��![]() ����
����
�������ߵĽ���ʽ����Ϊy=ax2+![]() ��
��
��A����1��2����������y=ax2+![]() �ϣ�
�ϣ�
��a+![]() =2��
=2��
���a=��![]() ��
��
�������ߵĺ�����ϵ����ʽΪy=��![]() x2+
x2+![]() ��
��
��2��������F�ڵ�һ����ʱ����ͼ1��
��y=0���![]() x2+
x2+![]() =0��
=0��
��ã�x1=3��x2=��3��
����C��������3��0����
��ֱ��AC�Ľ���ʽΪy=mx+n��
����![]() ��
��
��� ��
��
��ֱ��AC�Ľ���ʽΪy=��![]() x+
x+![]() ��
��
��������OEFG�ı߳�Ϊp����F��p��p����
����F��p��p����ֱ��y=��![]() x+
x+![]() �ϣ�
�ϣ�
�ੁ![]() p+
p+![]() =p��
=p��
���p=1��
����F��������1��1����
������F�ڵڶ�����ʱ��
ͬ���ɵã���F������Ϊ����3��3����
��ʱ��F�����߶�AC�ϣ�����ȥ��
������������F��������1��1����
��3������M��MH��DN��H����ͼ2��
��OD=t��OE=t+1��
����E�͵�C�غ�ʱֹͣ�˶�����0��t��2��
��x=tʱ��y=��![]() t+
t+![]() ����N��t����
����N��t����![]() t+
t+![]() ����DN=��
����DN=��![]() t+
t+![]() ��
��
��x=t+1ʱ��y=��![]() ��t+1��+
��t+1��+![]() =��
=��![]() t+1����M��t+1����
t+1����M��t+1����![]() t+1����ME=��
t+1����ME=��![]() t+1��
t+1��
��Rt��DEM��DM2=12+����![]() t+1��2=
t+1��2=![]() t2��t+2��
t2��t+2��
��Rt��NHM��MH=1��NH=����![]() t+
t+![]() ��������
��������![]() t+1��=
t+1��=![]() ��
��
��MN2=12+��![]() ��2=
��2=![]() ��
��
����DN=DMʱ��
����![]() t+
t+![]() ��2=
��2=![]() t2��t+2��
t2��t+2��
���t=![]() ��
��
����ND=NMʱ��
��![]() t+
t+![]() =
=![]() ��
��
���t=3��![]() ��
��
����MN=MDʱ��
![]() =
=![]() t2��t+2��
t2��t+2��
���t1=1��t2=3��
��0��t��2����t=1��
��������������DMN�ǵ���������ʱ��t��ֵΪ![]() ��3��
��3��![]() ��1��
��1��


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ABC��,��O�DZ�AC��һ������,��O��ֱ��MN��BC.��MN����ACB��ƽ�����ڵ�E,����ACB�����ƽ�����ڵ�F��
��1����֤��OE=OF��
��2����CE=12,CF=5,��OC�ij���
��3������O�ڱ�AC���˶���ʲôλ��ʱ,�ı���AECF�Ǿ��Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
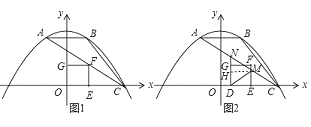
����Ŀ��ij������ҵ��Ҫ����һ��������ֲ�ijɻ��ʣ��Ըõ�������������ֲ�ɻ�������е���ͳ�ƣ�����������ͼ��ʾ��ͳ�Ʊ�������ͳ��ͼ�ṩ����Ϣ����������⣺
����������ɻ��Ƶ���ȶ���_________���ɻ�ĸ��ʹ���ֵΪ_______________��
���õ����Ѿ���ֲ��������5��ã�
��������������ɻ�___________��ã�
������õ����ƻ��ɻ�18����������磬��ô������ֲ��������Լ������ã�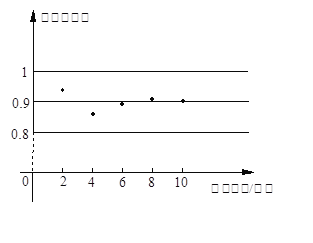
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��L�� ![]() ��x�ᡢy��ֱ���A��B���㣬��y������һ��
��x�ᡢy��ֱ���A��B���㣬��y������һ��
C��0��4��,����M��A����ÿ��1����λ���ٶ���x�������ƶ���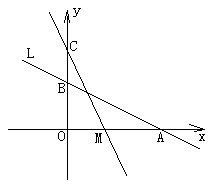
��1����A��B��������ꣻ
��2�����COM�����S��M���ƶ�ʱ��t֮��ĺ�����ϵʽ��
��3����tΪ��ֵʱ��COM�ա�AOB�������ʱM������ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������AOBC��ֱ������ϵ�У���A��y���ϣ���B��x���ϣ���֪��C�������ǣ�8��4����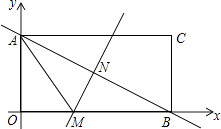
��1����Խ���AB����ֱ�ߵĺ�����ϵʽ��
��2���Խ���AB�Ĵ�ֱƽ����MN��x���ڵ�M������AM�����߶�AM�ij���
��3������P��ֱ��AB�ϵ�һ�����㣬����PAM������볤����OABC��������ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016�꣬ij�з��������ظɺ��������������پ����Լ��ˮ��Ϊ�˽������ˮ�������ijС����������10����ͥ������ˮ�������ͳ����ͼ���������10����ͥ������ˮ��������˵��������ǣ� ��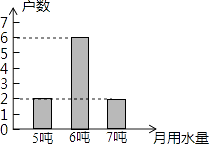
A.������6
B.�����6
C.ƽ������6
D.������4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��3����ʿ�����߳�չ�������ڶ�����Դ���ͣ��������綯��������������������£��������綯����������̵���������λ���ֱ�Ϊ��������
����Ʒ�� | ���� | ��ʱ�� | �ִ�С��SUV | �ݱ� | ����˫�� |
������̣���� | 665 | 500 | 470 | 500 | 450 |
A.665��470B.450��500C.500��470D.500��500
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У�AB=4��BC=5����ABC=60�㣬�Խ���AC��BD���ڵ�O������O��OE��AD����OE���ڣ� �� 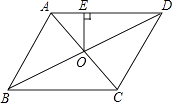
A.![]()
B.2 ![]()
C.2
D.2.5
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com