练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．用一个圆心角为120°，半径为3的扇形作一个圆锥的侧面，则这个圆锥的底面半径为（　　）
    A．1B．2

    分析 根据扇形的弧长公式求出弧长，根据圆锥的底面周长等于展开后扇形的弧长，根据周长公式求出半径即可．

    解答 解：扇形的弧长=$\frac{120π×3}{180}$
    =2π，
    圆锥的底面半径为：2π÷2π=1．
    故选：A．

    点评 考查了扇形的弧长公式、圆的周长公式，理解圆锥的底面周长等于展开后扇形的弧长是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    15．（1）计算：$\sqrt{12}$-3×（$\sqrt{3}$）-1+2sin60°
    （2）先化简：$\frac{1}{x-3}$•$\frac{{x}^{3}-6{x}^{2}+9x}{{x}^{2}-2x}$-$\frac{1-x}{2-x}$，然后再取一个你喜爱的x的值代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

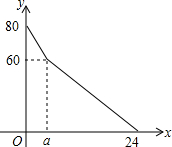    16．某超市开设了自助收银区，实施自助收银，以节省顾客的排队时间．某日上午10点，超市值班经理发现在自助收银区已经有80人在等待自助收银，此时仍有顾客不断前来排队等候．在自助收银区，假设顾客按固定的速度增加，每个收银口自助收银的速度也是固定的，其中每分钟新增排队人数为3人，每分钟每个收银口自助收银2人．
    （1）若10点后收银的前a分钟只开放4个收银口，10点后排队等候收银的人数y（人）与收银时间x（分钟）的关系如图所示．
    ①求a值；
    ②求超市在10点20分时，自助收银区排队等候收银的顾客人数．
    （2）超市有承诺：顾客排队不超过10分钟，即要在10点10分内让所有排队的顾客都能完成自助收银，以便后来的顾客能随到随收．请帮助值班经理计算一下10点后至少需要同时开放几个收银口？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．如图，已知∠1=70°，如果CD∥BE，那么∠B的度数为（　　）
    A．130°B．70°C．115°D．110°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．计算：（$\frac{1}{3}$）-1+|-2|+（$\sqrt{2}$-1）0=6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．中华人民共和国的陆地面积为9600000km2，9600000这个数用科学记数法表示为（　　）
    A．9.6×105B．96×105C．9.6×106D．96×106

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，在△ABC中，AD是BC边上的高，AE是BC边上的中线，cosC=$\frac{\sqrt{2}}{2}$，sinB=$\frac{1}{3}$，AD=1．
    （1）求BC的长；
    （2）求tan∠DAE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．“五一劳动节大酬宾！”，某商场设计的促销活动如下：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“50元”的字样．规定：在本商场同一日内，顾客每消费满300元，就可以在箱子里先后摸出两个球（第一次摸出后不放回）．商场根据两小球所标金额的和返还相等价格的购物券，购物券可以在本商场消费．某顾客刚好消费300元．
    （1）该顾客至多可得到70元购物券；
    （2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于50元的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：
    （1）（$\frac{1}{2}$）-2+$\root{3}{-8}$-20150； 
    （2）（x-2）2-（x+2）（x-3）．

    查看答案和解析>>

    同步练习册答案