
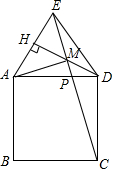
 如图,正方形ABCD,点E在正方形外侧且DE=CD,DH⊥AE,垂足为H交CE于M.
如图,正方形ABCD,点E在正方形外侧且DE=CD,DH⊥AE,垂足为H交CE于M.分析 (1)根据等腰三角形的想知道的∠DEC=∠DCE,得多AD=CD=ED,即AD=ED,根据等腰三角形的性质得到∠DEC+∠EDH=∠DCE+∠ADH=$\frac{180°-∠ADC}{2}$=$\frac{180°-90°}{2}$=45°,于是得到结论;
(2)连接BM,将△ABM绕B顺时针旋转90°,使M落在N处,A落在C处,则AM=CN,延长DE交BN于F,可得∠FCN=∠DCE,推出M,C,N三点共线,即△MBN是等腰直角三角形,根据勾股定理得到MN=$\sqrt{2}$BM,于是得到结论;
(3)在(2)中图,作DG⊥CE交CE于G,根据已知条件得到DC=2,PD=1,由勾股定理得到PC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,推出△DPN是等腰直角三角形,于是得到结论.
解答 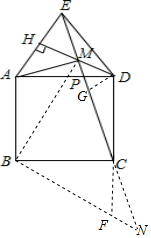 (1)证明:∵DE=CD,
(1)证明:∵DE=CD,
∴∠DEC=∠DCE,
∴AD=CD=ED,即AD=ED,
∵DH⊥AE,
∴∠EDH=∠ADH,
∵∠DEC+∠EDH=∠DCE+∠ADH=$\frac{180°-∠ADC}{2}$=$\frac{180°-90°}{2}$=45°,
∴∠CMD=45°;
(2)证明:连接BM,将△ABM绕B顺时针旋转90°,使M落在N处,A落在C处,
则AM=CN,延长DE交BN于F,可得
∠BAM=∠BAD+∠DAM=∠BCF+∠FCN,
∴∠FCN=∠DAM=∠DEC=∠DCE,
即∠FCN=∠DCE,
∴M,C,N三点共线,
即△MBN是等腰直角三角形,
∴MN=$\sqrt{2}$BM,
∵CN=AM=EM,
∴MN=CM+CN=CM+EM,
∴AM+CM=$\sqrt{2}$BM;
(3)解:在(2)中图,作DG⊥CE交CE于G,
∵正方形的边长为2,P是AD的中点,
∴DC=2,PD=1,PC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴DG=$\frac{PD•DC}{PC}$=$\frac{2×1}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
∵∠CMD=45°,∠DPN=90°,
∴△DPN是等腰直角三角形,
∴DM=$\sqrt{2}$DG=$\sqrt{2}$×$\frac{2\sqrt{5}}{5}$=$\frac{2\sqrt{10}}{5}$.
点评 本题考查了正方形的性质,等腰直角三角形的性质,旋转的性质,正确的作出辅助线是解题的关键.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
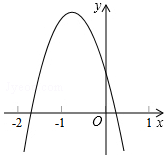 已知二次函数y=ax2+bx+c的图象如图所示.下列结论:
已知二次函数y=ax2+bx+c的图象如图所示.下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
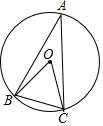 如图,⊙O是△ABC的外接圆,⊙O的半径为2,∠A=30°,则BC=( )
如图,⊙O是△ABC的外接圆,⊙O的半径为2,∠A=30°,则BC=( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\frac{1}{3}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com