
����Ŀ������֪��������һ��ͼ�Σ�ͨ�����ֲ�ͬ�ķ�������������������Եõ�һ�����ֵ�ʽ������ͼ1�����Եõ�(a+2b)(a+b)��a2+3ab+2b2�����������⣺
(1)д��ͼ2������ʾ����ѧ��ʽ_____��
(2)����(1)�����õ��Ľ��ۣ������������⣺��֪a+b+c��9��ab+bc+ac��26����a2+b2+c2��ֵ��
(3)С��ͬѧ��2�ű߳�Ϊa�������Ρ�3�ű߳�Ϊb�������Ρ�5�ű߳�Ϊa��b�ij�����ֽƬƴ����һ�������Σ���ô�ó����νϳ�һ�ߵı߳�Ϊ���٣�
(4)С��ͬѧ����x�ű߳�Ϊa�������Σ�y�ű߳�Ϊb�������Σ�z�ű߳��ֱ�Ϊa��b�ij�����ֽƬƴ����һ�����Ϊ(25a+7b)(2a+5b)�����Σ���9x+10y+6��
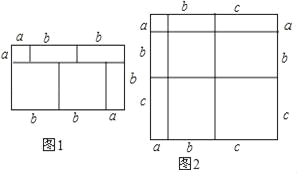
���𰸡�(1)(a+b+c)2��a2+b2+c2+2ab+2bc+2ca��(2)29��(3)�ϳ���һ�߳�Ϊ2a+3b��(4)806��
��������
(1)ֱ����������ε����,Ȼ���ٸ��������ε����=�����ε����֮����⼴��;
(2)��a+b+c=9,ab+bc+ac=26����(1)�еõ��Ĺ�ϵʽ,Ȼ����м��㼴��;
(3)���г������ε�����Ĵ���ʽ,Ȼ��ֽ����ʽ,�ɵõ����ε����߳�
(4)�����ε����xa2+yb2+zab=(25a+7b)(9a+5b),Ȼ���������ʽ�˶���ʽ�������(25a+7
b)(2a+45b)�Ľ��,�Ӷ��õ�x��y��z��ֵ,���뼴�����
�⣺(1)�����ε�����ɱ�ʾΪ��(a+b+c)2��
����������a2+b2+c2+2ab+2bc+2ca��
����(a+b+c)2��a2+b2+c2+2ab+2bc+2ca��
�ʴ�Ϊ��(a+b+c)2��a2+b2+c2+2ab+2bc+2ca��
(2)��(1)��֪��a2+b2+c2��(a+b+c)2��2(ab+bc+ca)��92��26��2��81��52��29��
(3)����������2a2+5ab+3b2��(2a+3b)(a+b)��
���Գ����εı߳�Ϊ2a+3b��a+b��
���Խϳ���һ�߳�Ϊ2a+3b��
(4)�߳����ε������xa2+yb2+zab��(25a+7b)(2a+5b)��50a2+14ab+125ab+35b2��50a2+139ab+35b2��
��x��50��y��35��z��139��
��9x+10y+6��450+350+6��806��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017��11��11�գ��Žܲμ���ij����������Ƴ齱���.��ͼ��ʾ��4�����Ϸֱ�д�ж�Ӧ��Ʒ�ļ�ֵΪ10Ԫ��15Ԫ��20Ԫ����лл�ݹ���������.
����������1���ƣ���ô�����н��ĸ���Ϊ ������15Ԫ�����Ͻ�Ʒ�ĸ���Ϊ .
����������2���ƣ��ҵ�һ�η������Ʋ��ٲμ��´η��ƣ��û���״ͼ���б����г��齱�����еȿ�����������������Ʒ��ֵ������30Ԫ�ĸ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
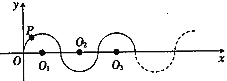
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У��뾶��Ϊ1����λ���ȵİ�Բ![]() ��
��![]() ��
��![]() �����һ��ƽ�������ߣ���
�����һ��ƽ�������ߣ���![]() ��ԭ��
��ԭ��![]() ���������������������˶����ٶ�Ϊÿ��
���������������������˶����ٶ�Ϊÿ��![]() ����λ���ȣ����2019��ʱ����
����λ���ȣ����2019��ʱ����![]() ��������____��
��������____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2��bx��c��ͼ����ͼ��������������ȷ����( )

A. abc��0 B. ��3a��c��0
C. b2��4ac��0 D. ���ú���ͼ������ƽ��2����λ�����õ������ߵĽ���ʽΪy��ax2��c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
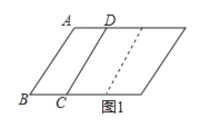
����Ŀ����ͼ1����ֱ֪��![]() ����
����![]() ��
��![]() ��ֱ��
��ֱ��![]() �ϣ���
�ϣ���![]() ��
��![]() ��ֱ��
��ֱ��![]() �ϣ���AB//CD����
�ϣ���AB//CD����![]() ���ֲ������߶�
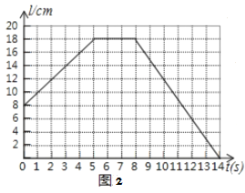
���ֲ������߶�![]() ����������ƽ���ƶ����м�ֹͣһ��ʱ�������������ƽ���ƶ���ͼ2��ӳ��
����������ƽ���ƶ����м�ֹͣһ��ʱ�������������ƽ���ƶ���ͼ2��ӳ��![]() �ij���
�ij���![]() ��ʱ��
��ʱ��![]() �ı仯���仯���������
�ı仯���仯���������
��1�����߶�![]() ��ʼƽ��֮ǰ��
��ʼƽ��֮ǰ��![]() _______
_______![]() ��
��
��2���߶�![]() ������ƽ����_______
������ƽ����_______![]() ������ƽ�Ƶ��ٶ���______
������ƽ�Ƶ��ٶ���______![]() ��
��
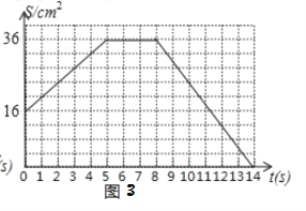
��3��ͼ3��ӳ�˱仯������![]() �����
�����![]() ��ʱ��
��ʱ��![]() �仯�������
�仯�������
��ƽ����![]() ��
��![]() ֮��ľ���Ϊ_______
֮��ľ���Ϊ_______![]() ��
��
�ڵ�![]() ʱ�����S��ֵΪ_____
ʱ�����S��ֵΪ_____![]() ��
��
�۵�![]() ʱ��ֱ��д��
ʱ��ֱ��д��![]() ����
����![]() �ĺ�����ϵʽ______(���Բ�����)��
�ĺ�����ϵʽ______(���Բ�����)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y��ax2��bx��cͼ���һ������ͼ�����A����3��0�����Գ���Ϊֱ��x����1�������ĸ���������b2��4ac����2a��b��0����a��b��c��0��������B����![]() ��y1����C����
��y1����C����![]() ��y2��Ϊ����ͼ���ϵ���������y1��y2��������ȷ������___________��
��y2��Ϊ����ͼ���ϵ���������y1��y2��������ȷ������___________��
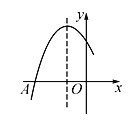
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ù����ۣ���ͼ1�����Լ��һ������Ĵ�С�Ƿ����Ҫ����֪�����۵������Ǿ�Ϊ90�㣬�ߴ���ͼ����λ��cm��������״���������������ʱ����ͬʱ����ͼ1��ʾ��A��B��E�����Ӵ��㣬����Ĵ�С�ͷ���Ҫ��ͼ2�ǹ�����O��A��B��E����Ľ���ʾ��ͼ�������������ֱ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ�����ܣ�ƽ��ÿ����۳�20�裬ÿ��ӯ��40Ԫ��Ϊ������ӯ����������ٿ�棬���Ծ�����ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣����ÿ�軨��ÿ��1Ԫ������ƽ��ÿ��ɶ��۳�2�裮
��1��������ƽ��ÿ��Ҫӯ��1200Ԫ��ÿ�軨��Ӧ���۶���Ԫ��
��2��ÿ�軨�ܽ��Ͷ���Ԫʱ������ƽ��ÿ��ӯ����࣬�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱ���ABC�У�
��1����ͼ1����DΪ�߶�BC�е㣬�߶�AD����ֱ��AB�ĶԳ��߶�Ϊ�߶�AE������DE�����BDE�Ķ�����
��2������DΪ�߶�BC��һ���㣨����B��C�غϣ�������AD�����߶�AD�Ƶ�D��ʱ����ת60���õ��߶�DE������BE.
�ٸ���������ͼ2�в�ȫͼ�Σ�
��С��ͨ���۲졢��֤������²⣺�ڵ�D�˶��Ĺ����У�����CD=BE.�����С��֤��CD=BE.
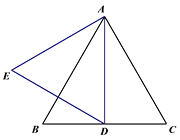
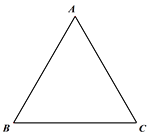
ͼ1 ͼ2
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com