
分析 (1)根据一次函数图象上点的坐标特征求出点A、B的坐标,再根据两点间的距离公式即可求出结论;
(2)根据点A的坐标利用反比例函数图象上点的坐标特征求出k值,此题得解.
解答 解:(1)∵正比例函数y=-$\frac{1}{2}$x图象上的点A、B的坐标分别为(4,m)、(n,2),
∴m=-$\frac{1}{2}$×4,2=-$\frac{1}{2}$n,
∴m=-2,n=-4,
∴点A的坐标为(4,-2),点B的坐标为(-4,2),
A、B两点间的距离AB=$\sqrt{(-4-4)^{2}+[2-(-2)]^{2}}$=4$\sqrt{5}$.
(2)∵反比例函数y=$\frac{k}{x}$的图象过点A(4,-2),
∴-2=$\frac{k}{4}$,解得:k=-8,
∴反比例函数的解析式为y=-$\frac{8}{x}$.
点评 本题考查了反比例函数图象上点的坐标特征以及一次函数图象上点的坐标特征,根据一次函数图象上点的坐标特征求出点A、B的坐标是解题的关键.


科目:初中数学 来源: 题型:解答题
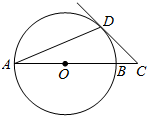 AB是⊙O的直径,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°.
AB是⊙O的直径,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
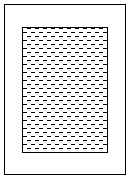 如图,用一张高为30cm,宽为20cm的长方形打印纸打印文档,如果左、右的页边距都为xcm,上、下页边距比左、右页边距多1cm.
如图,用一张高为30cm,宽为20cm的长方形打印纸打印文档,如果左、右的页边距都为xcm,上、下页边距比左、右页边距多1cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
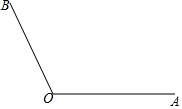 如图,已知∠AOB=120°.点C在∠AOB的内部,且∠BOC=30°;OP是∠AOB的角平分线.
如图,已知∠AOB=120°.点C在∠AOB的内部,且∠BOC=30°;OP是∠AOB的角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
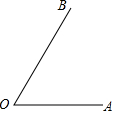 如图,∠AOB.(1)用尺规作出∠AOB的平分线OD;
如图,∠AOB.(1)用尺规作出∠AOB的平分线OD;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,CD是△ABC的高,∠A=22.5°,边AC的垂直平分线交AB于点E,EF⊥BC,交CD于点G,垂足为F.
已知,如图,CD是△ABC的高,∠A=22.5°,边AC的垂直平分线交AB于点E,EF⊥BC,交CD于点G,垂足为F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com