
 如图是一个4×4的正方形网格,图中所标示的7个角的角度之和等于585°.
如图是一个4×4的正方形网格,图中所标示的7个角的角度之和等于585°. 分析 仔细观察图形,我们可以发现△ABC≌△AZV,根据全等三角形的性质可得∠1=∠AVZ,进而可得∠1+∠7=180°,同理可得:∠2+∠6=180°,∠3+∠5=180°,∠4=45°,然后可得答案.
解答 解:仔细观察图形,我们可以发现:
∵AB=AZ,BC=ZV,∠B=∠Z,
∴△ABC≌△AZV,
∴∠1+∠7=180°,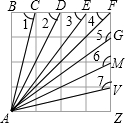
同理可得:
∠2+∠6=180°,
∠3+∠5=180°,
∠4=45°,
所以说图示的7个角的度数和为∠1+∠7+∠2+∠6+∠3+∠5+∠4=180°+180°+180°+45°=585°,
故答案为:585°.
点评 本题考查了全等三角形对应角相等的性质,求证全等三角形,找出对应角是解决本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
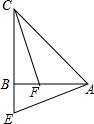 在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF.
在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
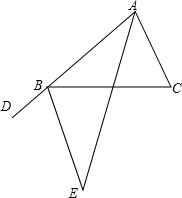 完成下面证明:如图,B是射线AD上一点,AE平分∠DAC,∠DAC=∠C=∠CBE
完成下面证明:如图,B是射线AD上一点,AE平分∠DAC,∠DAC=∠C=∠CBE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:P为正方形ABCD内一点,△ABP绕点A顺时针旋转后得到的△ADM.
已知:P为正方形ABCD内一点,△ABP绕点A顺时针旋转后得到的△ADM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
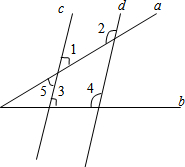 直线c、d分别被直线a、b所截,且∠3+∠4=180°,求证:∠2+∠5=180°.
直线c、d分别被直线a、b所截,且∠3+∠4=180°,求证:∠2+∠5=180°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com