
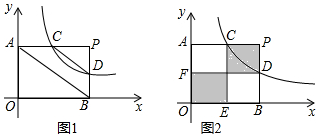
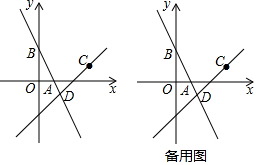
���� �٢���A��0��b����B��a��0������C��$\frac{k}{b}$��b����D��a��$\frac{k}{a}$������ʾPC��PD��AC��BD�ij�������ã�$\frac{PC}{AC}$=$\frac{PD}{BD}$����CD��AB��
�۽�k=$\frac{ab}{2}$����C��$\frac{k}{b}$��b����D��a��$\frac{k}{a}$�����ɵã�C��$\frac{a}{2}$��b����D��a��$\frac{b}{2}$������֪CΪPA���е㣬DΪPB���е㣬��ƽ�к����ƣ��������������ζ�Ӧ�ߵıȵ��ڶ�Ӧ�ߵıȵý��ۣ�
�ܸ�������Ӱ���ֵ�����е�ʽ�ɵã�k=$\frac{ab}{2}$������D�������ɵý��ۣ�
��� �⣺����A��0��b����B��a��0������C��$\frac{k}{b}$��b����D��a��$\frac{k}{a}$����
��PC=a-$\frac{k}{b}$=$\frac{ab-k}{b}$��
PD=b-$\frac{k}{a}$=$\frac{ab-k}{a}$��
��$\frac{PC}{AC}$=$\frac{\frac{ab-k}{b}}{\frac{k}{b}}$=$\frac{ab-k}{k}$��
$\frac{PD}{BD}$=$\frac{\frac{ab-k}{a}}{\frac{k}{a}}$=$\frac{ab-k}{k}$��
��$\frac{PC}{AC}$=$\frac{PD}{BD}$��
��CD��AB��
���Ԣٲ���ȷ������ȷ��
����ͼ1����P��a��b����k=$\frac{ab}{2}$��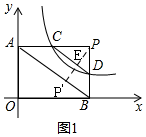
��C��$\frac{a}{2}$��b����D��a��$\frac{b}{2}$����
��CΪPA���е㣬DΪPB���е㣬
��CD�ǡ�PAB����λ�ߣ�
��CD��AB��
���PCD�ס�PAB��
��P��PP���CD����CD��E����AB��P�䣬
�ɡ�PCD�ס�PAB�ã�$\frac{PC}{PA}=\frac{PE}{PP��}$=$\frac{1}{2}$��
��PE=EP�䣬
���ѡ�PCD��CD�۵���P��һ������AB�ϣ�
���Ԣ���ȷ��
���ɢ٣���A��0��b����B��a��0������C��$\frac{k}{b}$��b����D��a��$\frac{k}{a}$����
��OE=$\frac{k}{b}$��BD=$\frac{k}{a}$��PC=a-$\frac{k}{b}$��PD=b-$\frac{k}{a}$��
��S����PCGD=S����GFOE��
��$\frac{k}{b}$��$\frac{k}{a}$=��a-$\frac{k}{b}$����b-$\frac{k}{a}$����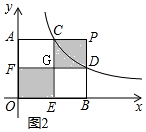
$\frac{{k}^{2}}{ab}$=ab-k-k+$\frac{{k}^{2}}{ab}$��
ab=2k��
��k=$\frac{ab}{2}$��
��D��a��$\frac{b}{2}$����
��BD=$\frac{b}{2}$��
��DΪPB�е㣻
���Ԣ���ȷ��
���Ա�����ȷ���ǣ��ڢۢܣ�
�ʴ�Ϊ���ڢۢܣ�
���� ���⿼���˷���������ϵ��k�ļ������塢���������Ƶ����ʺ��ж���ƽ���߷��߶γɱ������������۱任�����ʣ����Ѷȣ�������A��B��������꣬�����ô������ʾC��D����������ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���ߣ�cm�� | 172 | 173 | 175 | 176 |
| ���������� | 2 | 6 | 3 | 5 |
| A�� | 173cm��173cm | B�� | 174cm��174cm | C�� | 173cm��174cm | D�� | 174cm��175cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 70�� | B�� | 135�� | C�� | 140�� | D�� | 55�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1000•sin���� | B�� | $\frac{1000}{sin��}$�� | C�� | 1000•cos���� | D�� | $\frac{1000}{cos��}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪���ڡ�ABC�У�D��EΪAC��AB�ϵĵ㣬BD��CE�ཻ��O��ȡAB���е�F������OF����AD=$\frac{1}{2}$CD��AE=$\frac{1}{2}$BE
��֪���ڡ�ABC�У�D��EΪAC��AB�ϵĵ㣬BD��CE�ཻ��O��ȡAB���е�F������OF����AD=$\frac{1}{2}$CD��AE=$\frac{1}{2}$BE�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
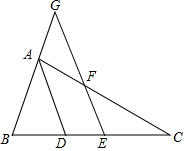 ��ͼ����ABC�У�ADƽ�֡�BAC��EF��BA�ӳ����ڵ�G����CFE=��G��
��ͼ����ABC�У�ADƽ�֡�BAC��EF��BA�ӳ����ڵ�G����CFE=��G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com