
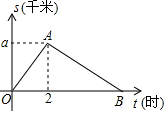
 某单位在小绿谷举办“民族团结一家亲”徒步活动,某人从起点出发,以4千米/小时的平均速度走了2小时到达终点,之后再沿原路返回,设此人离开起点的路程s(千米)与步行时间t(小时)之间的函数关系如图所示.根据图象提供信息,解答下列问题:
某单位在小绿谷举办“民族团结一家亲”徒步活动,某人从起点出发,以4千米/小时的平均速度走了2小时到达终点,之后再沿原路返回,设此人离开起点的路程s(千米)与步行时间t(小时)之间的函数关系如图所示.根据图象提供信息,解答下列问题:分析 (1)根据路程=速度×时间即可求出a值;
(2)①根据速度=路程÷时间求出此人返回时的速度,再根据路程=8-返回时的速度×时间即可得出AB所在直线的函数解析式;
②令①中的函数关系式中s=0,求出t值即可.
解答 解:(1)a=4×2=8.
(2)①此人返回的速度为(8-5)÷(1.75-$\frac{8-5}{4}$)=3(千米/小时),
AB所在直线的函数解析式为s=8-3(t-2)=-3t+14.
②当s=-3t+14=0时,t=$\frac{14}{3}$.
答:此人走完全程所用的时间为$\frac{14}{3}$小时.
点评 本题考查了一次函数的应用,解题的关键是:(1)根据路程=速度×时间求出a值;(2)①根据路程=8-返回时的速度×时间列出s与t之间的函数解析式;②令s=0求出t值.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形OABC在平面直角坐标系中,A、C两点的坐标分别为A(6,0),C(0,-3),直线y=-$\frac{3}{4}$x与BC边相交于D点,过原点的抛物线y=ax2+bx经过A、D两点.
如图,矩形OABC在平面直角坐标系中,A、C两点的坐标分别为A(6,0),C(0,-3),直线y=-$\frac{3}{4}$x与BC边相交于D点,过原点的抛物线y=ax2+bx经过A、D两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
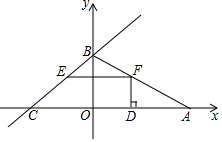 如图,已知直线y=$\frac{3}{4}$x+3与坐标轴交于B,C两点,点A是x轴正半轴上一点,并且S△ABC=15,点F是线段AB上一动点(不与端点重合),过点F作FE∥x轴,交BC于E.
如图,已知直线y=$\frac{3}{4}$x+3与坐标轴交于B,C两点,点A是x轴正半轴上一点,并且S△ABC=15,点F是线段AB上一动点(不与端点重合),过点F作FE∥x轴,交BC于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com