
分析 根据衍生点的定义,若点A1的坐标为(a,b),分别计算点A2,A3,A4,A5,A6,A7的坐标,根据计算结果得到这些点的坐标每6个一循环,则可利用2015=335×6+5,可判断点A2015的坐标与点A5相同,即为(a,$\frac{b-1}{b}$).
解答 解:若点A1的坐标为(a,b),
点A1的衍生点为A2的坐标为(-a+1,1-$\frac{1}{b}$),即A2(-a+1,$\frac{b-1}{b}$);
点A2的衍生点为A3的坐标为(a-1+1,1-$\frac{1}{\frac{b-1}{b}}$),即A3(a,-$\frac{1}{b-1}$);
点A3的衍生点为A4的坐标为(-a+1,1-$\frac{1}{-\frac{1}{b-1}}$),即A4(-a+1,b);
点A4的衍生点为A5的坐标为(a-1+1,1-$\frac{1}{b}$),即A5(a,$\frac{b-1}{b}$);
点A5的衍生点为A6的坐标为(-a+1,1-$\frac{1}{\frac{b-1}{b}}$),即A6(-a+1,-$\frac{1}{b-1}$);
点A6的衍生点为A7的坐标为(a-1+1,1-$\frac{1}{-\frac{1}{b-1}}$),即A7(a,b),
…
而2015=335×6+5,
所以点A2015的坐标与点A5相同,即为(a,$\frac{b-1}{b}$).
∵点A1的坐标为(2,-1),
∴a=2,b=-1.
∵a=2,$\frac{b-1}{b}$=$\frac{-1-1}{-1}$=2,
∴点A2015的坐标为(2,2),
故答案为:(2,2).
点评 本题考查点的坐标的变化规律,将数学周期的思想进行了初步渗透,属于中档题,利用衍生点的定义得出规律:这些点的坐标每6个一循环,即点A1与点A7重合是解题关键.


科目:初中数学 来源: 题型:解答题
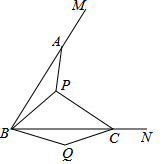 如图,已知∠MBN=60°,在BM,BN上分别截取BA=BC,P是∠MBN内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
如图,已知∠MBN=60°,在BM,BN上分别截取BA=BC,P是∠MBN内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com