
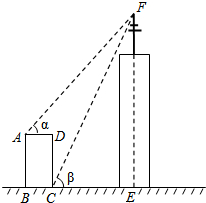
 如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.
如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.分析 (1)延长AD交FE于G,设CE=x,根据正切的概念用含x的代数式表示GF、EF,根据题意列出方程,解方程即可;
(2)把已知数据代入(1)中的关系式,根据特殊角的三角函数值和二次根式的运算法则计算即可.
解答 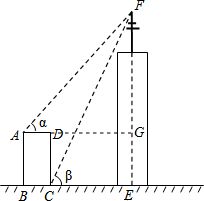 解:(1)延长AD交FE于G,
解:(1)延长AD交FE于G,
设CE=x,则DG=x,
在Rt△AFG中,tanα=$\frac{GF}{GA}$,
∴GF=AG•tanα=(x+18)tanα,
在Rt△FCE中,tanβ=$\frac{EF}{EC}$,
FE=x•tanβ,
∵FE=FG+EG,
∴x•tanβ=(x+18)tanα+78,
解得,x=$\frac{18tanα+78}{tanβ-tanα}$,
即CE=$\frac{18tanα+78}{tanβ-tanα}$;
(2)FE=x•tanβ
=$\frac{18tanα+78}{tanβ-tanα}$×tanβ
=$\frac{18×tan30°+78}{tan60°-tan30°}×tan60°$
=$\frac{18×\frac{\sqrt{3}}{3}+78}{\sqrt{3}-\frac{\sqrt{3}}{3}}×\sqrt{3}$
=9$\sqrt{3}$+117
≈133(m).
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握余角俯角的概念、熟记锐角三角函数的定义是解题的关键.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
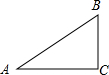 如图,在△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
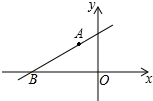 如图,直线y=kx+b经过A(-1,2)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-2x的解集为-$\sqrt{7}$<x<-1.
如图,直线y=kx+b经过A(-1,2)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-2x的解集为-$\sqrt{7}$<x<-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
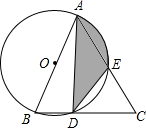 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交于点D、E,连接DE、AD.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交于点D、E,连接DE、AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com