Question

在四边形ABCD中，AC与BD相交于点O，如果只给出条件“AB∥CD”，那么还不能判定四边形ABCD为平行四边形，给出以下5个说法：
①如果再加上条件“∠DBA=∠CAB”，那么四边形ABCD为平行四边形．
②如果再加上条件“AB=CD”，那么四边形ABCD为平行四边形；
③如果再加上条件“∠DAB=∠DCB”，那么四边形ABCD为平行四边形；
④如果再加上条件“BC=AD”，那么四边形ABCD是平行四边形；
⑤如果再加上条件“AO=CO”，那么四边形ABCD为平行四边形；
其中正确的说法有

1. A.
   5个
2. B.
   4个
3. C.
   3个
4. D.
   2个

Answer 1

C
分析：①根据已知易证得OA=OB，OC=OD，但不能判定四边形ABCD为平行四边形；
②利用一组对边平行且相等的四边形是平行四边形，即可判定四边形ABCD为平行四边形；
③由AB∥CD，∠DAB=∠DCB，易证得∠ABC=∠ADC，根据有两组对边分别相等的四边形是平行四边形，即可判定四边形ABCD是平行四边形；
④因为若AB∥CD，BC=AD，此四边形也可以是等腰梯形，故不能判定四边形ABCD是平行四边形；
⑤此题可以通过证明三角形全等，证得AB=CD，继而证得此四边形是平行四边形．
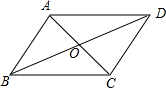
解答：①∵AB∥CD，
∴∠DBA=∠BDC，∠CAB=∠ACD，
∵∠DBA=∠CAB，
∴∠ACD=∠BDC，
∴OA=OB，OC=OD，
∴不能判定四边形ABCD为平行四边形；
故错误；
②∵AB=CD，AB∥CD，
∴四边形ABCD为平行四边形，
故正确；
③∵AB∥CD，
∴∠DAB+∠ADC=180°，∠ABC+∠DCB=180°，
∵∠DAB=∠DCB，
∴∠ADC=∠ABC，
∴四边形ABCD为平行四边形；
故正确；
④∵若AB∥CD，BC=AD，此四边形也可以是等腰梯形，
∴不能判定四边形ABCD为平行四边形；
故错误；
⑤∵AB∥CD，
∴∠BAO=∠DCO，∠ABO=∠CDO，
在△AOB和△COD中，
，
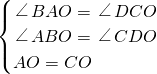
∴△AOB≌△COD（AAS），
∴AB=CD，
∴四边形ABCD是平行四边形；
故正确；
故选C．
点评：此题考查了平行四边形的判定．注意真命题需要证明，假命题只要举反例即可．解题时还要注意数形结合思想的应用．
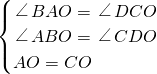