
【题目】已知函数![]() .
.
![]() 抛物线的开口向____ 、对称轴为直线_ _、顶点坐标__ _;
抛物线的开口向____ 、对称轴为直线_ _、顶点坐标__ _;
![]() 当
当![]() ___ _时,函数有最___ 值,是__ _;
___ _时,函数有最___ 值,是__ _;
![]() 当
当![]() _ _ ______时,
_ _ ______时,![]() 随
随![]() 的增大而增大;当
的增大而增大;当![]() ____ __时,
____ __时,![]() 随
随![]() 的增大而减小;
的增大而减小;
![]() 该函数图象可由
该函数图象可由![]() 的图象经过怎样的平移得到的?
的图象经过怎样的平移得到的?
【答案】![]() 下
下 ![]() ;
; ![]()
![]() ;大;
;大;![]() ;
; ![]()
![]() ;
; ![]() 向左
向左![]() 个,向上平移
个,向上平移![]() 个单位
个单位
【解析】
(1),(2),(3)由于是二次函数,由此可以确定函数的图像的形状,根据二次项系数可以确定开口方向,根据抛物线的顶点式解析式可以确定其顶点的坐标,对称轴及增减性;
(4)根据左加右减,上加下减可得出答案.
解:由二次函数![]() 可得
可得
(1)抛物线的开口方向向下,对称轴为直线x=-2,顶点坐标为(-2,9).
(2)当x=-2时,函数y有最大值,是9.
(3)当x<-2时,函数y随x的增大而增大,当x>-2时,函数y随x的增大而减小.
(4)函数![]() 的图像先向左平移2个单位,再向上平移9个单位即可得到
的图像先向左平移2个单位,再向上平移9个单位即可得到![]() .
.
故答案为![]() 下
下 ![]() ;
; ![]()
![]() ;大;
;大;![]() ;
; ![]()
![]() ;
; ![]() 向左
向左![]() 个,向上平移
个,向上平移![]() 个单位.
个单位.


科目:初中数学 来源: 题型:
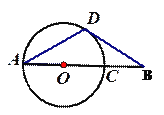
【题目】如图,AD是⊙O的弦,AC是⊙O直径,⊙O的切线BD交AC的延长线于点B,切点为D,∠DAC=30°.
(1)求证:△ADB是等腰三角形;
(2)若BC= ![]() ,则AD的长为 .
,则AD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
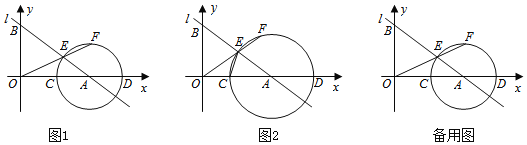
【题目】如图1,直线l:![]() 与x轴交于点
与x轴交于点![]() ,与y轴交于点B,点C是线段OA上一动点
,与y轴交于点B,点C是线段OA上一动点![]() 以点A为圆心,AC长为半径作
以点A为圆心,AC长为半径作![]() 交x轴于另一点D,交线段AB于点E,连结OE并延长交
交x轴于另一点D,交线段AB于点E,连结OE并延长交![]() 于点F.
于点F.
![]() 求直线l的函数表达式和
求直线l的函数表达式和![]() 的值;
的值;
![]() 如图2,连结CE,当
如图2,连结CE,当![]() 时,
时,
![]() 求证:
求证:![]() ∽
∽![]() ;
;
![]() 求点E的坐标;
求点E的坐标;
![]() 当点C在线段OA上运动时,求
当点C在线段OA上运动时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
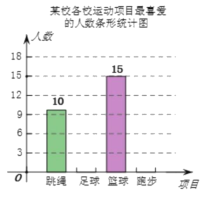
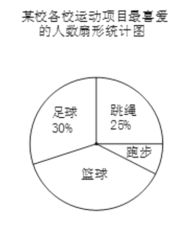
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)在扇形统计图中,“篮球”部分所对应的圆心角度数为__ ;
(4)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
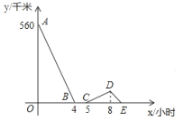
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为![]() 小时,两车之间的距离为
小时,两车之间的距离为![]() 千米,图中折线表示
千米,图中折线表示![]() 与
与![]() 之间的函数图象.当快车到达甲地时,慢车离甲地的距离为__________千米.
之间的函数图象.当快车到达甲地时,慢车离甲地的距离为__________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教委为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,启动了“学生阳光体育运动”,其中有一项是短跑运动,短跑运动可以锻炼人的灵活性,增强人的爆发力,因此张明和李亮在课外活动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
成绩统计分析表
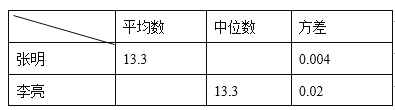
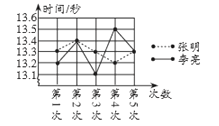
(1)张明第2次的成绩为__________秒;
(2)请补充完整上面的成绩统计分析表;
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁? 请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是![]() 的直径,点P在BA的延长线上,PD切
的直径,点P在BA的延长线上,PD切![]() 于点D,过点B作
于点D,过点B作![]() ,交PD的延长线于点C,连接AD并延长,交BE于点E.
,交PD的延长线于点C,连接AD并延长,交BE于点E.
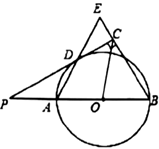
(Ⅰ)求证:AB=BE;
(Ⅱ)连结OC,如果PD=2![]() ,∠ABC=60°,求OC的长.
,∠ABC=60°,求OC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com