
| A. | a2+a2=a4 | B. | (a2)3=a5 | C. | 2a2-a2=2 | D. | a5•a2=a7 |
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
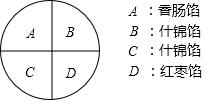 大年夜吃饺子是中华民族的传统习俗,妈妈为洋洋准备了四只饺子:一只香肠陷A,两只什锦馅B和C,一只红枣馅D,四只饺子除内部馅料不同外,其他均一切相同,洋洋喜欢吃什锦馅的饺子.
大年夜吃饺子是中华民族的传统习俗,妈妈为洋洋准备了四只饺子:一只香肠陷A,两只什锦馅B和C,一只红枣馅D,四只饺子除内部馅料不同外,其他均一切相同,洋洋喜欢吃什锦馅的饺子.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
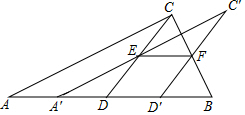 如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF.
如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
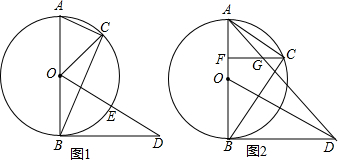
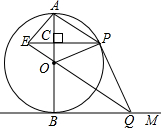 如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.
如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
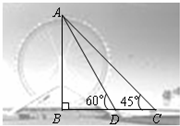 2016年,合肥万达主题乐园开门迎客,合肥万达全国诸多万达乐园中惟一拥有摩天轮的项目,亦是园区内天际线的重要组成部分,是园区内观赏风光的最佳选择.某校数学兴趣小组要测量摩天轮的高度,如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50m至D处,测得最高点A的仰角为60°,求该兴趣小组测得的摩天轮的高度AB.
2016年,合肥万达主题乐园开门迎客,合肥万达全国诸多万达乐园中惟一拥有摩天轮的项目,亦是园区内天际线的重要组成部分,是园区内观赏风光的最佳选择.某校数学兴趣小组要测量摩天轮的高度,如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50m至D处,测得最高点A的仰角为60°,求该兴趣小组测得的摩天轮的高度AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
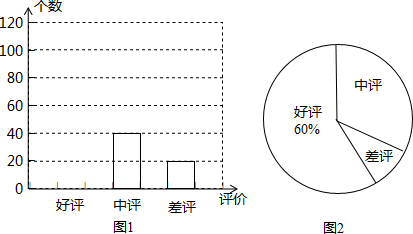
 老师想知道学生每天在上学的路上要花多少时间,于是让大家将每天来学校的单程时间写在纸上.如图是全班30名学生上学单程所花时间的条形统计图:
老师想知道学生每天在上学的路上要花多少时间,于是让大家将每天来学校的单程时间写在纸上.如图是全班30名学生上学单程所花时间的条形统计图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
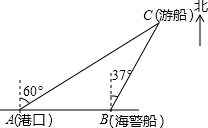 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻事故,立即出发了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以50海里每小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻事故,立即出发了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以50海里每小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com