
【题目】如图,![]() 是
是![]() 内接三角形,点D是BC的中点,请仅用无刻度的直尺,分别按下列要求画图.
内接三角形,点D是BC的中点,请仅用无刻度的直尺,分别按下列要求画图.

(1)如图1,画出弦AE,使AE平分∠BAC;
(2)如图2,∠BAF是![]() 的一个外角,画出∠BAF的平分线.
的一个外角,画出∠BAF的平分线.
【答案】(1)见解析;(2)见解析
【解析】
(1)连接OD,延长OD交![]() 于E,连接AE,根据垂径定理可得
于E,连接AE,根据垂径定理可得![]() ,根据圆周角定理可得∠BAE=∠CAE,即可得答案;
,根据圆周角定理可得∠BAE=∠CAE,即可得答案;
(2)连接OD,延长OD交![]() 于E,连接AE,反向延长OD,交
于E,连接AE,反向延长OD,交![]() 于H,作射线AH,由(1)可知∠BAE=∠CAE,由HE是直径可得∠EAH=∠BAE+∠BAH=90°,根据平角的定义可得∠CAE+∠FAH=90°,即可证明∠BAH=∠FAH,可得答案.
于H,作射线AH,由(1)可知∠BAE=∠CAE,由HE是直径可得∠EAH=∠BAE+∠BAH=90°,根据平角的定义可得∠CAE+∠FAH=90°,即可证明∠BAH=∠FAH,可得答案.
(1)如图,连接OD,延长OD交![]() 于E,连接AE,
于E,连接AE,
∵OE为半径,D为BC中点,
∴![]() ,
,
∴∠BAE=∠CAE,
∴AE为∠BAC的角平分线,弦![]() 即为所求.
即为所求.

(2)如图,连接OD,延长OD交![]() 于E,连接AE,反向延长OD,交
于E,连接AE,反向延长OD,交![]() 于H,作射线AH,
于H,作射线AH,
∵HE是![]() 直径,点A在
直径,点A在![]() 上,
上,
∴∠EAH=∠BAE+∠BAH=90°,
∴∠CAE+∠FAH=90°,
由(1)可知∠BAE=∠CAE,
∴∠BAH=∠FAH,
∴AH平分∠BAF,射线![]() 即为所求.
即为所求.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
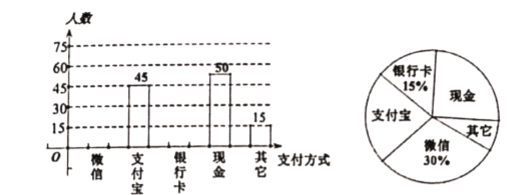
(1)这次活动共调查了多少人;
(2)将条形统计图补充完整;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了矩形后,数学活动小组开展了探究活动.如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,先以
上,先以![]() 为折痕将
为折痕将![]() 点往右折,如图2所示,再过点
点往右折,如图2所示,再过点![]() 作
作![]() ,垂足为
,垂足为![]() ,如图3所示.
,如图3所示.

(1)在图3中,若![]() ,则
,则![]() 的度数为______,
的度数为______,![]() 的长度为______.
的长度为______.
(2)在(1)的条件下,求![]() 的长.
的长.
(3)在图3中,若![]() ,则
,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区开展了“行车安全,方便居民”的活动,对地下车库作了改进.如图,这小区原地下车库的入口处有斜坡AC长为13米,它的坡度为i=1:2.4,AB⊥BC,为了居民行车安全,现将斜坡的坡角改为13°,即∠ADC=13°(此时点B、C、D在同一直线上).
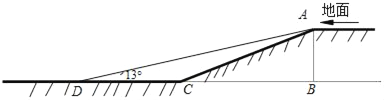
(1)求这个车库的高度AB;
(2)求斜坡改进后的起点D与原起点C的距离(结果精确到0.1米).
(参考数据:sin13°≈0.225,cos13°≈0.974,tan13°≈0.231,cot13°≈4.331)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图矩形![]() 是矩形ABCD的“减半”矩形.
是矩形ABCD的“减半”矩形.
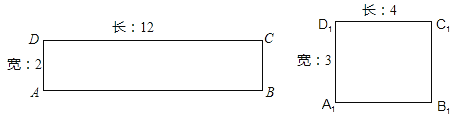
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为![]() 的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的解析式是y=x2﹣(k+2)x+2k﹣2.
(1)求证:此抛物线与x轴必有两个不同的交点;
(2)若抛物线与直线y=x+k2﹣1的一个交点在y轴上,求该二次函数的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解决问题:
材料1:在研究数的整除时发现:能被5、25、125、625整除的数的特征是:分别看这个数的末一位、末两位、末三位、末四位即可,推广成一条结论;末![]() 位能被
位能被![]() 整除的数,本身必能被
整除的数,本身必能被![]() 整除,反过来,末
整除,反过来,末![]() 位不能被
位不能被![]() 整除的数,本身也不可能被
整除的数,本身也不可能被![]() 整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
![]() ,
,![]() 为整数,
为整数,![]() 能被25整除
能被25整除
![]() ,
,![]() 不为整数,
不为整数,![]() 不能被625整除
不能被625整除
材料2:用奇偶位差法判断一个数能否被11这个数整除时,可把这个数的奇位上的数字与偶位上的数字分别加起来,再求它们的差,看差能否被11整除,若差能被11整除,则原数能被11整除,反之则不能.
(1)若![]() 这个三位数能被11整除,则
这个三位数能被11整除,则![]() ;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
(2)若一个六位数p的最高位数字为5,千位数字是个位数字的2倍,且这个数既能被125整除,又能被11整除,求这个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com