
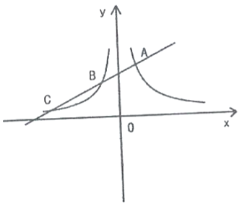
【题目】如图,直线![]() 与
与![]() 的图象交于点
的图象交于点![]() ,直线
,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点.
两点.
(1)直接写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2) 点![]() 在平面内,若以
在平面内,若以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形是平行四边形,求符合条件的所有
四点为顶点的四边形是平行四边形,求符合条件的所有![]() 点的坐标.
点的坐标.
【答案】(1)![]() ; (2)
; (2)![]() 或
或![]() 或P(0,5)
或P(0,5)
【解析】
(1)现将![]() 代入
代入![]() 可得a的值以及A点的坐标,再将A点坐标代入
可得a的值以及A点的坐标,再将A点坐标代入![]() 中,可得m的值,再将
中,可得m的值,再将![]() 、
、![]() 代入
代入![]() 可得b、c的值
可得b、c的值
(2)根据平行四边形的性质对边平行可得出直线OP的解析式,再设![]() 点坐标,根据平行四边形对变相等,列出方程即可求解
点坐标,根据平行四边形对变相等,列出方程即可求解
解:(1)将![]() 代入
代入![]() 得:
得:![]()
∴A![]()
将A![]() 代入
代入![]() 中,可得:
中,可得:![]() ,解得:
,解得:![]() ;
;
将![]() 代入
代入![]() 得:
得:![]()
∴![]()
将![]() 代入
代入![]() 得:
得:![]()
∴![]()
故答案为:![]() ;
;
(2)由题意,若以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形是平行四边形,则可得
四点为顶点的四边形是平行四边形,则可得
①当OP∥AB;
∴![]() ,OP=AB;
,OP=AB;
∵OP过原点
∴OP的函数解析式为正比例函数
∴![]()
设![]()
又∵OP=AB,![]()
∴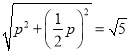
解得:p=2或p=﹣2
∴![]() 或
或![]()
②当AB为对角线时,∵A(1,3),O(0,0),B(-1,2),
![]() 解得:
解得:![]() ,
,
∴点P3的坐标为(0,5);
∴综上所述:当以A,B,O,P四点为顶点的四边形是平行四边形时,P点的坐标为(-2,-1),(2,1)或(0,5).


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
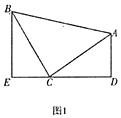
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
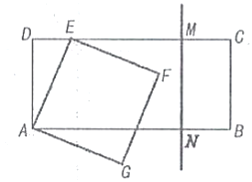
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,以
个单位的速度运动,以![]() 为一边在
为一边在![]() 的右下方作正方形
的右下方作正方形![]() .同时垂直于
.同时垂直于![]() 的直线
的直线![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,设运动时间为
个单位的速度运动,设运动时间为![]() 秒,当
秒,当![]() ________.秒时,直线
________.秒时,直线![]() 和正方形
和正方形![]() 开始有公共点
开始有公共点
查看答案和解析>>
科目:初中数学 来源: 题型:
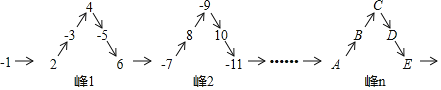
【题目】将一列有理数﹣1,2,﹣3,4,﹣5,6,…如图所示有序排列,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中C的位置是有理数_____,﹣2019应排在A、B、C、D、E中的_____位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B、C为数轴上三点,若点C到点A的距离是点C到点B的距离的2倍,则称点C是(A,B)的奇异点,例如图1中,点A表示的数为﹣1,点B表示的数为2,表示1的点C到点A的距离为2,到点B的距离为1,则点C是(A,B)的奇异点,但不是(B,A)的奇异点.
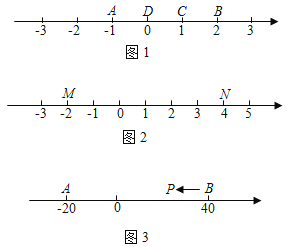
(1)在图1中,直接说出点D是(A,B)还是(B,C)的奇异点;
(2)如图2,若数轴上M、N两点表示的数分别为﹣2和4,
①若(M,N)的奇异点K在M、N两点之间,则K点表示的数是 ;
②若(M,N)的奇异点K在点N的右侧,请求出K点表示的数.
(3)如图3,A、B在数轴上表示的数分别为﹣20和40,现有一点P从点B出发,向左运动.若点P到达点A停止,则当点P表示的数为多少时,P、A、B中恰有一个点为其余两点的奇异点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种盛酒的桶,已知10个大桶加上2个小桶可以盛酒6斛(斛,音hu,是古代的一种容量单位),3个大桶加上15个小桶也可以盛酒6斛.
(1)求1个大桶可盛酒多少斛?
(2)分析2个大桶加上3个小桶可以盛酒2斛吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() .
.
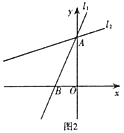
(1)求证:![]() .
.
(2)已知直线![]() 与
与![]() 轴交于
轴交于![]() 点,将直线
点,将直线![]() 绕着
绕着![]() 点顺时针旋转45°至
点顺时针旋转45°至![]() ,如图2,求
,如图2,求![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
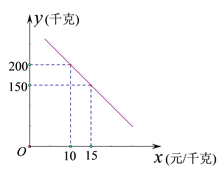
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间的函数关系如图所示.
(元/千克)之间的函数关系如图所示.
(1)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com