
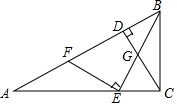
 如图,△ABC中,∠ACB=90°,CD⊥AB于D,点E在AC上,BE交CD于G,EF⊥BE交AB于F,CE:BC:AE=1:2:3.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,点E在AC上,BE交CD于G,EF⊥BE交AB于F,CE:BC:AE=1:2:3.分析 (1)根据两边成比例夹角相等两三角形相似即可判断.
(2)只要证明GE=GC,GB=GC即可.
(3)由∠A=∠BCD,推出tan∠CBD=tan∠A=$\frac{1}{2}$=$\frac{BD}{CD}$,设BD=m,则CD=2m.设BG=CG=x,
在Rt△BDG中,根据BG2=BD2+DG2,得到x2=a2+(2a-x)2,求得x=$\frac{5}{4}$a,所以tan∠DBG=$\frac{DG}{BD}$=$\frac{\frac{3}{4}a}{a}$=$\frac{3}{4}$,根据$\frac{EF}{BE}$=tan∠EBF,即可解决问题.
解答 证明:(1)∵CE:BC:AE=1:2:3,设EC=a,BC=2a,AE=3a则AC=4a,
∴$\frac{EC}{BC}$=$\frac{BC}{AC}$=2,∵∠BCE=∠ACB,
∴△BCE∽△ACB,
(2)∵△BCE∽△ACB,CD⊥AB,
∴∠ABC=∠BEC,∠BDC=90°
∵∠ABC+∠BCD=90°,∵∠ACD+∠BCD=90°,
∴∠GEC=∠GCE,
∴GE=GC,同理可证GB=GC,
∴BG=EG.
(3)∵∠A=∠BCD,
∴tan∠CBD=tan∠A=$\frac{1}{2}$=$\frac{BD}{CD}$,设BD=m,则CD=2m.设BG=CG=x,
在Rt△BDG中,∵BG2=BD2+DG2,
∴x2=a2+(2a-x)2,
∴x=$\frac{5}{4}$a,
∴tan∠DBG=$\frac{DG}{BD}$=$\frac{\frac{3}{4}a}{a}$=$\frac{3}{4}$,
∴$\frac{EF}{BE}$=tan∠EBF=$\frac{3}{4}$.
点评 本题考查相似三角形的判定和性质、锐角三角函数、勾股定理、等腰三角形的判定和性质等知识,解题的关键是熟练掌握相似三角形的判定和性质,学会利用参数构建方程解决问题,属于中考常考题型.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:选择题
 乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )
乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )| A. | 1.5小时 | B. | 1.8小时 | C. | 2小时 | D. | 2.5小时 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2与|-2| | B. | -2与$\sqrt{(-2)^{2}}$ | C. | -2与-$\frac{1}{2}$ | D. | -2与$\root{3}{-8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1004<a<1005 | B. | 1004≤a<1005 | ||
| C. | 1004<a<1005或-1005≤a<-1004 | D. | 1004≤a<1005或-1005<a≤-1004 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
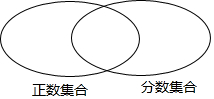 把下列各数填在相应的圆圈集合内:
把下列各数填在相应的圆圈集合内:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com